Trata-se de uma técnica de coloração que acompanha pares conjugados dentro de uma UNIDADE (linha, coluna ou QM). As “cores” ALTERNADAS mostram qual delas será a solução do Sudoku. Sempre procurar por números que formem pares conjugados em uma UNIDADE (o número poderá estar em uma célula com mais de dois números possíveis).
Exemplo 1:
No sudoku abaixo iniciou-se a coloração na célula D1. Atribuiu-se a cor verde ao número “1” e a cor azul ao número “8”, em seguida acompanha-se os pares, alternando-se as cores. Os candidatos marcados em vermelho na célula I9 podem ser excluídos, pois enxergam as séries verde/azul para o mesmo número (mesmas regras da técnica de coloração).
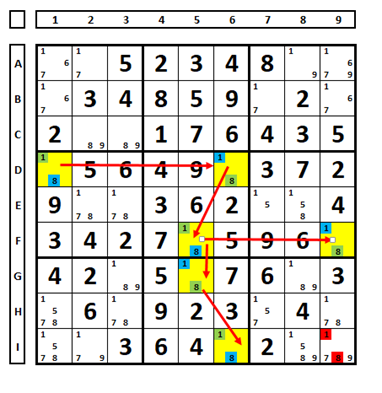
Exemplo 2:
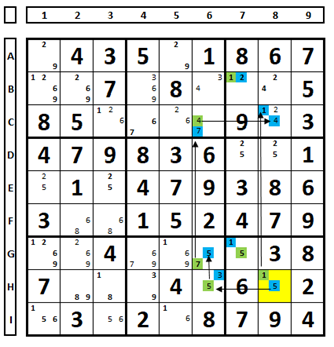
A partir da célula marcada em amarelo, foram marcados os números, alternando com verde e azul.
Na célula C8 tivemos dois números marcados em azul (1,4). Como não pode haver dois números resolvendo uma célula, ambos devem ser excluídos, ficando o número “2” como solução desta célula do Sudoku. A série azul pode ser excluída, pois na mesma UNIDADE ou em uma célula, não pode haver dois números da mesma série.
Exemplo 3:
Começando na célula I5, chega-se a seguinte situação: na célula H1 há as duas cores, logo o número “5” pode ser excluído desta célula, pois a solução estará entre os números “2” e “7”. Observe as cores opostas para o número “5” (em H2 e H8), o que também permite a exclusão do número “5” em H1.
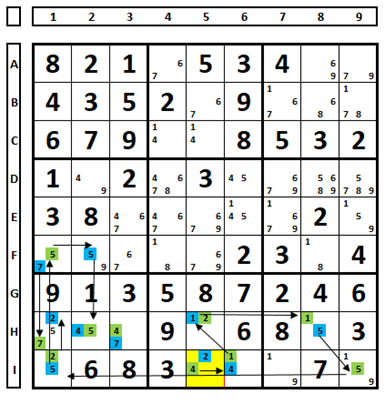
Pode-se estabelecer as seguintes regras:

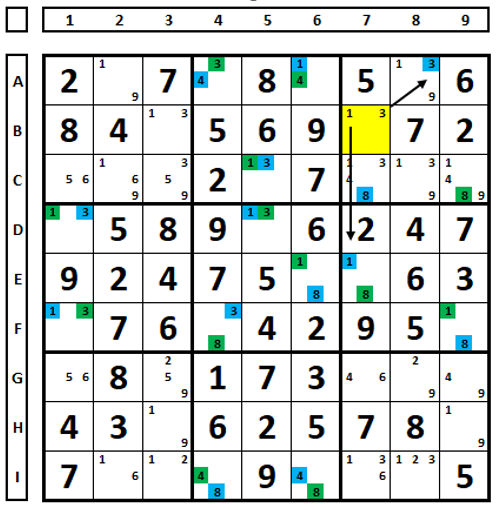
5. Célula esvaziada por cor: Quando os números de uma célula não marcada com cores puderem “enxergar” estes mesmos números em outras células já coloridas, e a cor for a mesma, esta cor não corresponde a solução do Sudoku. No caso abaixo, os números da célula B7 “enxergam” as células A8 e E7 e os números correspondentes estão marcados em azul. Por consequência, os números marcados em azul não são solução deste Sudoku. Por quê? Se a célula B7 fosse colorida, a partir das cores já postas, ambos os números seriam coloridos de verde, o que contrariaria a regra.
Outro exemplo. A série azul é resposta para o Sudoku.
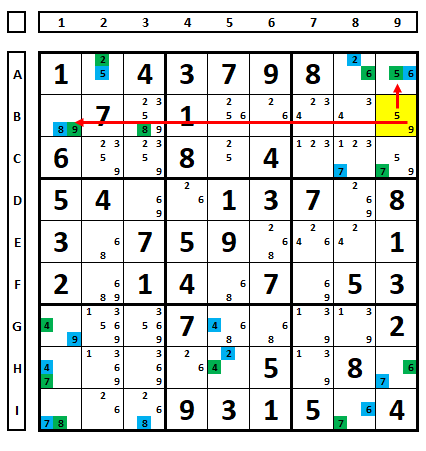
Um último exemplo, para demonstrar que muitas vezes não há necessidade de decorar técnicas, ou lembrar de todas, mas observar o que está acontecendo no Sudoku. Observe o Sudoku abaixo, onde as células foram marcadas alternadamente com azul/marrom.

Observe que, alternando as cores é possível eliminar o número “7” em H4, pois enxerga H3 (marrom) e C4 (azul).
Mas observe, em H4 restou o número “9” como solução do Sudoku, mas não se sabe se da série azul ou marrom. Será marcada em verde e feitas as exclusões.
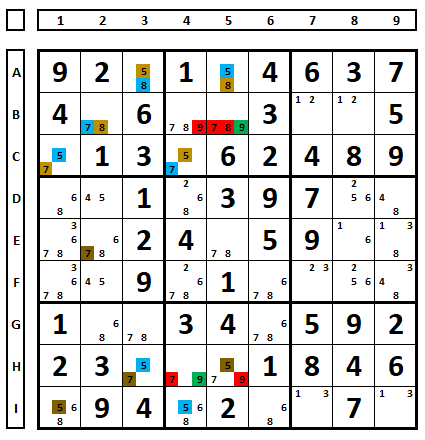
Continuando a colorir, os números “7” e “8” da célula B5 foram excluídos, pois o número “9” é solução nesta célula.
O número “8” marrom em A5 força o número “8” em E5 ser azul e o número “7” marrom. Como os números “7” em E2 e E5 são marcados em marrom, a série azul é solução deste Sudoku.
Exemplo da importância da boa observação.
No Sudoku abaixo, há a série verde/azul com o seguinte resultado, que aparentemente não leva a nenhuma solução.
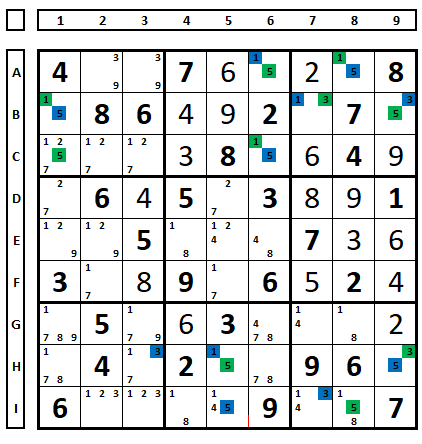
Mas, ao observar a linha I, vê-se que há uma contradição se a série azul for solução para este Sudoku. Vamos escolher a série azul como solução do sudoku.

Na linha I, as células I2 e I3 conterão o número “2” o que contraria a regra. Logo a série verde é solução deste Sudoku.
Repetindo: muitas vezes as técnicas apresentam soluções que não são as “regras da técnica”, como acima. É sempre útil observar se não há conclusões extras a serem tiradas (a partir do aprimoramento do leitor na observação das oportunidades).

