This is a coloring technique that follows conjugate pairs within a UNIT (row, column, or box). The ALTERNATING “colors” show which one will be the Sudoku solution. Always look for numbers that form conjugate pairs in a UNIT (the number may be in a cell with more than two possible numbers).
Example 1:
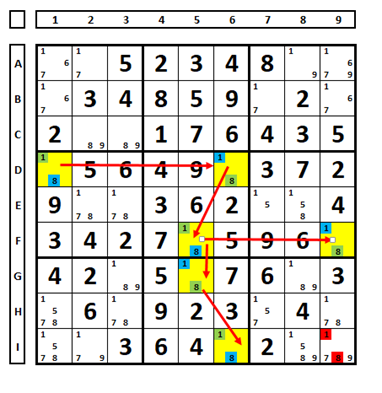
In the Sudoku below, coloring started in cell D1. The number “1” was assigned the green color and the number “8” was assigned the blue color, then the pairs are followed, alternating the colors. The candidates marked in red in cell I9 can be eliminated, as they see the green/blue pairs (same rules as coloring technique).
Example 2:
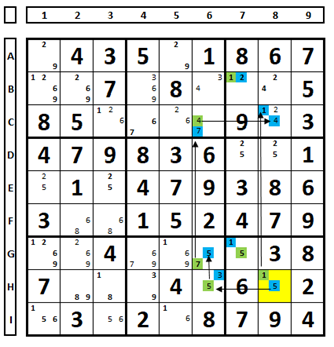
Starting from the cell marked in yellow, numbers were marked alternating between green and blue.
In cell C8, we had two numbers marked in blue (1,4). Since there cannot be two numbers solving a cell, both should be excluded, leaving the number “2” as the solution for this Sudoku cell. The blue series can be excluded because in the same UNIT or cell, there cannot be two numbers from the same series.
Example 3:
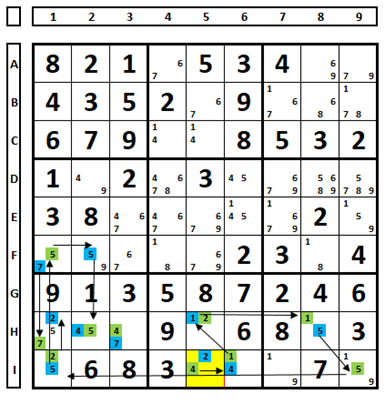
Starting from the cell I5, the following situation is reached: in cell H1 there are both colors, so the number “5” can be excluded from this cell, since the solution will be between the numbers “2” and “7”. Note the opposite colors for the number “5” (in H2 and H8), which also allows for the exclusion of the number “5” in H1.
One can establish the following rules::

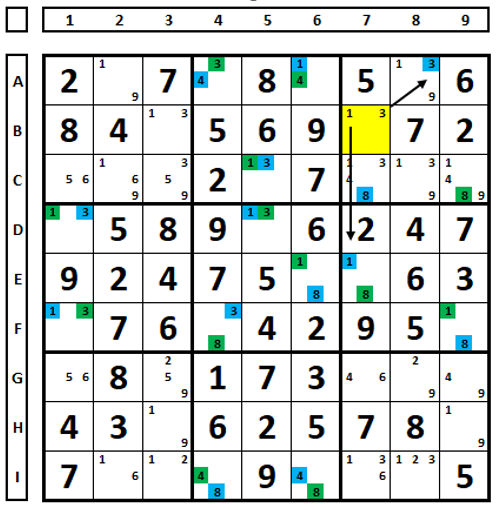
Empty cell by color: When the numbers in an uncolored cell can “see” the same numbers in other colored cells, and the color is the same, this color is not a solution to the Sudoku. In the example below, the numbers in cell B7 “see” cells A8 and E7 and the corresponding numbers are marked in blue. Therefore, the numbers marked in blue are not a solution to this Sudoku. Why? If cell B7 were colored, based on the already placed colors, both numbers would be colored green, which would violate the rule.
Another example. The blue series is the solution for the Sudoku:
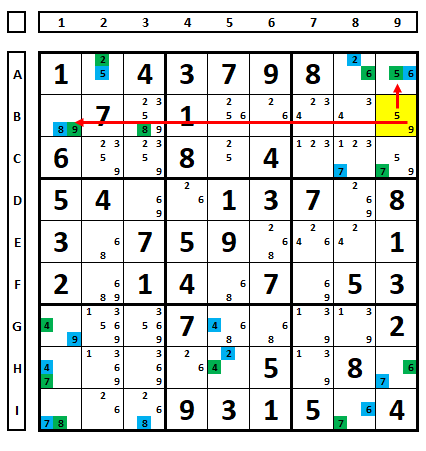
One last example, to demonstrate that many times there is no need to memorize techniques, or remember all of them, but to observe what is happening in the Sudoku. Observe the Sudoku below, where the cells have been alternately marked with blue/brown:

Note that, alternating the colors, it is possible to eliminate the number “7” in H4, as it “sees” H3 (brown) and C4 (blue).
But note that, in H4, the number “9” remains as the solution of the Sudoku, but it is not known whether it belongs to the blue or brown series.
It will be marked in green and exclusions will be made:
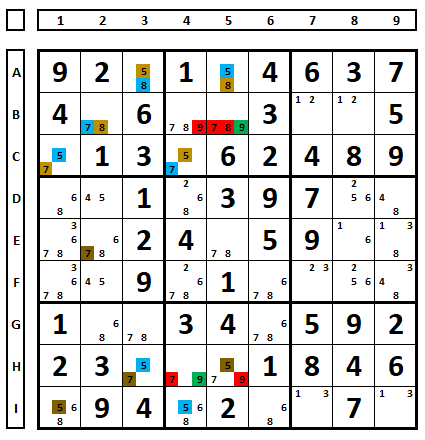
Continuing to color, the numbers “7” and “8” from cell B5 were excluded, as the number “9” is a solution in this cell.
The brown number “8” in A5 forces the number “8” in E5 to be blue and the number “7” to be brown. As the numbers “7” in E2 and E5 are marked in brown, the blue series is this Sudoku solution.
Example of the importance of good observation.
In the Sudoku below, there is the green/blue series with the following result, which apparently does not lead to any solution:
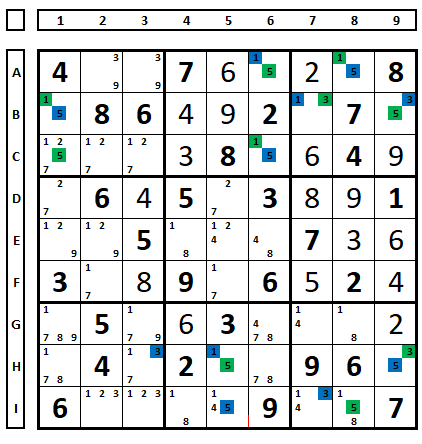
But, by observing row I, we see that there is a contradiction if the blue series is the solution to this Sudoku. Let’s choose the blue series as the solution to the sudoku:

In row I, cells I2 and I3 will contain the number “2”, which violates the rule. Therefore, the green series is the solution to this Sudoku.
Many times techniques present solutions that are not “technique rules”, as shown above. It is always useful to observe if there are any extra conclusions to be drawn (based on the reader’s improved observation skills). The book shows some extra non-technical conclusions.

