Caracteriza-se por um QM (3×3), onde quatro células (ou mais) não contém o candidato, deixando um padrão com o candidato na forma de L, T ou +, chamado dobradiça. As células devem exergar um par bloqueado (do mesmo número) em uma linha ou coluna externa ao QM. Com isto é possível excluir um candidato que aviste as extremidades dos dois conjuntos.
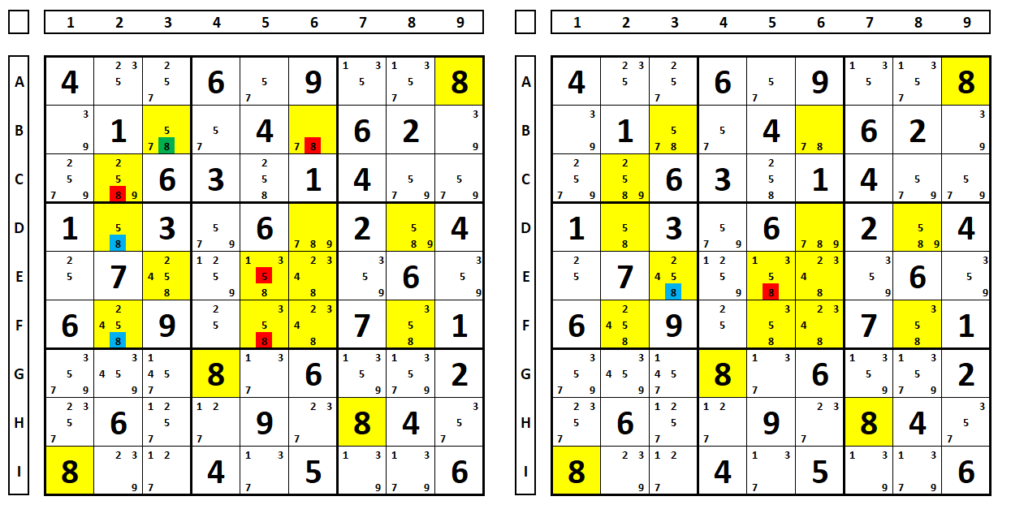
No exemplo abaixo, no QM9, as células G7, G8, H7 e H8, formam o retângulo vazio (não há número “7”) e o L (invertido). Se qualquer um dos números “7” das células G9 e I9 for solução do sudoku eles enxergam a extremidade do par bloqueado (A1/A9) na linha A, sendo então este número na célula A1 solução do sudoku, permitindo eliminar este número na célula I1. Caso este número na célula I7 seja a solução, isto também excluí este número na célula I1.
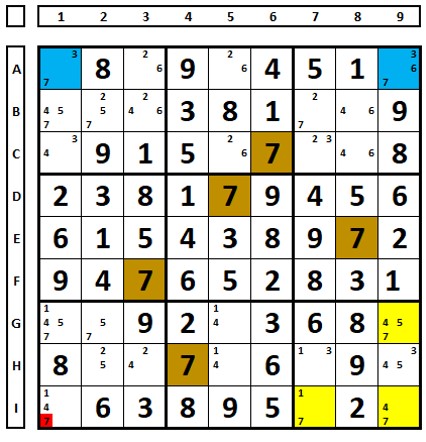
Outro exemplo em “L”: qualquer escolha para o número “8” em C1 ou G1, o número “8” em G7 será excluído.
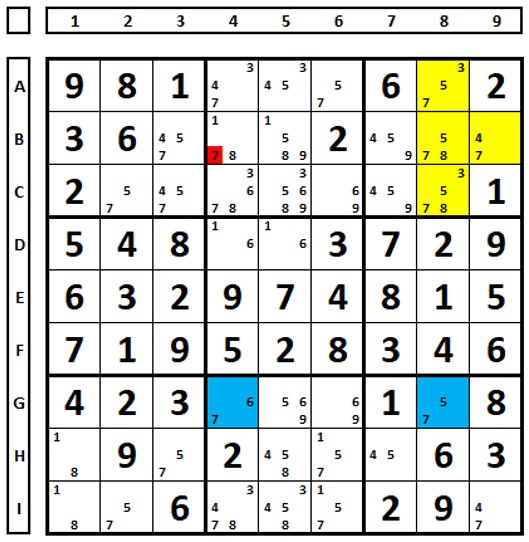
Um exemplo em “T”: para qualquer escolha do número “7” nas células azuis, este será excluído em B4.
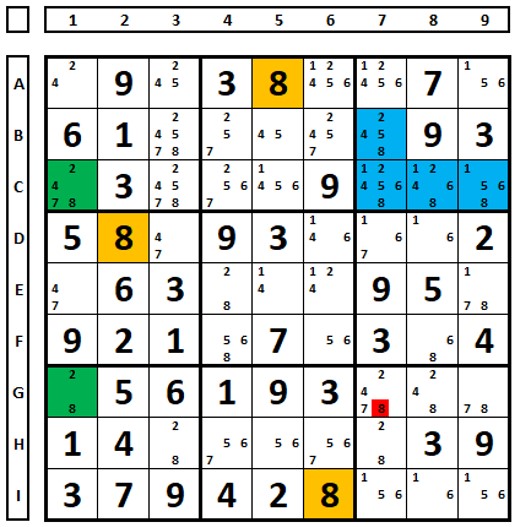
Exemplo com “+”, para o número “5”, qualquer escolha nas células verdes irá excluir este número na célula B3.
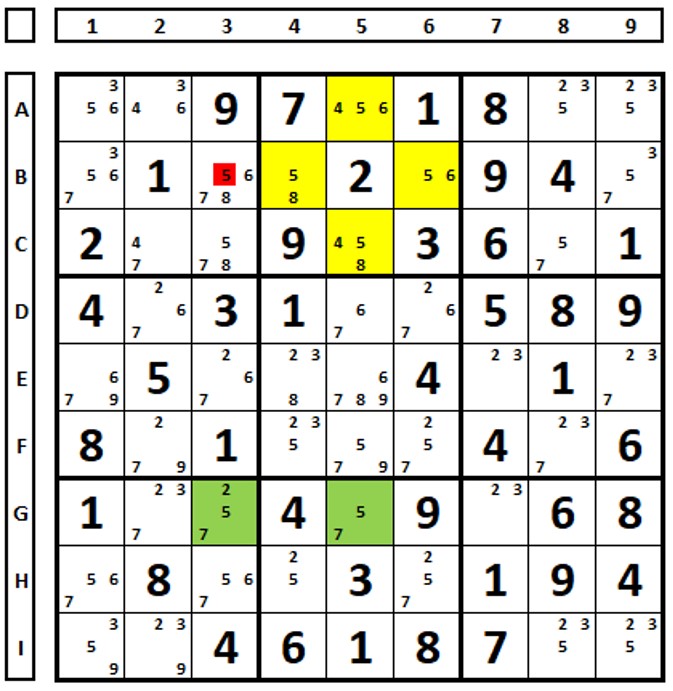
No Sudoku abaixo é possível eliminar os dois números “4” marcados em vermelho. Aqui há dois ER. Tente.
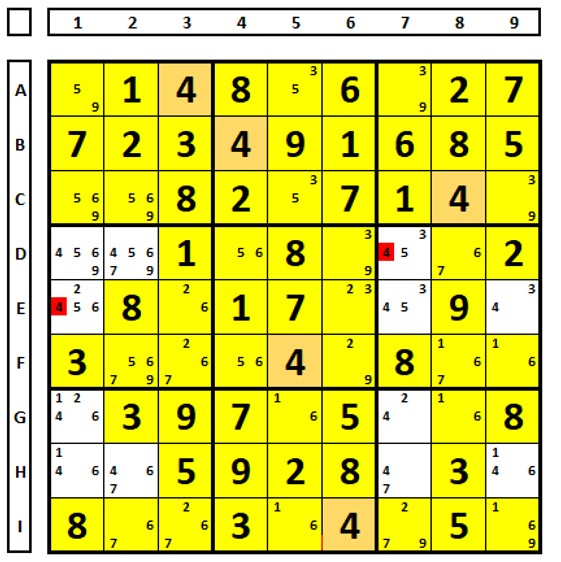
Muitas vezes ao se tentar a solução do Sudoku por determinada técnica esta não funciona, deve-se então observar se não há outras conclusões a serem tiradas, vamos chamar isto de "dica extra-técnica".
Prestar atenção as possibilidades, a partir das técnicas conhecidas, permite excluir/incluir números em determinadas células. Examinando o Sudoku abaixo, para o número “9”.

É possível ver uma situação “parecida” com ER. AS células marcadas em azul no QM3 não formam um ER. O que acontece quando elas “enxergam” células marcadas em amarelo? Ao escolher-se o número “9” em A2 ou H2, ocorrem as situações abaixo. As posições em verde nos QM3, QM6 e QM9 mostram as possíveis posições deste número. O número “9” pode ser excluído na célula C9.
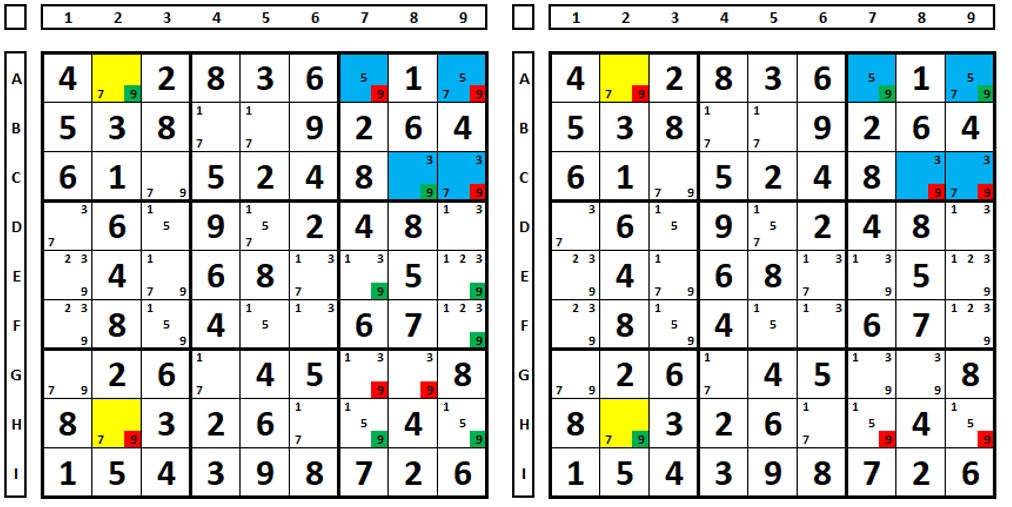
Repetindo. Sempre deve-se estar atento a situações semelhantes. Neste mesmo sudoku, examinando o número “6”. Há um falso ER (nem tão falso assim) entre as células marcadas em verde e azul, mas o que acontece ao se considerar um ER e testar?

Ao escolher-se a célula D4 e depois a D9 como solução do sudoku, verifica-se que os números “6” são comuns para eliminação em D1, D2, F2 e F3.
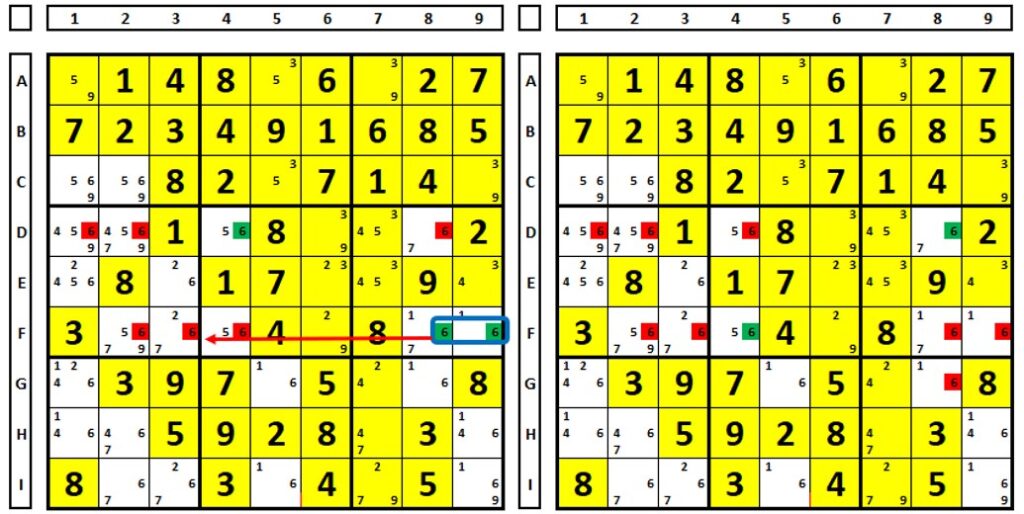
No exemplo abaixo, para o número “8”. No QM4 há duas células (D2 e F2) direcionadas para duas células em amarelo no QM1 (figura da esquerda). Se uma das duas for solução deste sudoku, haverá as eliminações em vermelho. Se a célula E3 for solução (figura da direita), haverá as eliminações em vermelho. A eliminação em comum (D5) poderá ser realizada.