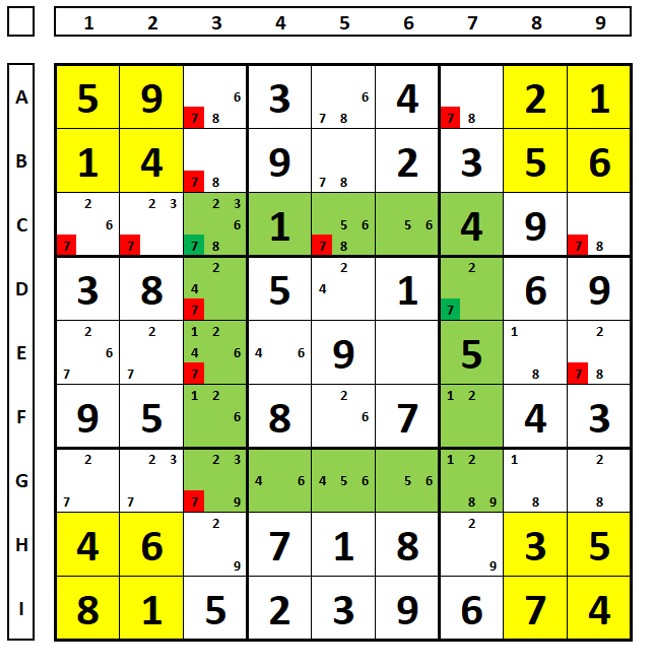
Invariante 1:
Em todos os sudokus acontece o seguinte, vamos direto a um exemplo.
Nas regiões amarelas há os números 1,2,3,4,5,7,8,9. Não há o número “6”.
O mesmo se repete na região azul.
Poderiam constar todos os nove números. O importante é que cada número aparece o mesmo número de vezes nas casas amarelas e azuis.

Outro exemplo. Todos os números (de 1 a 9) estão contemplados nos dois conjuntos.
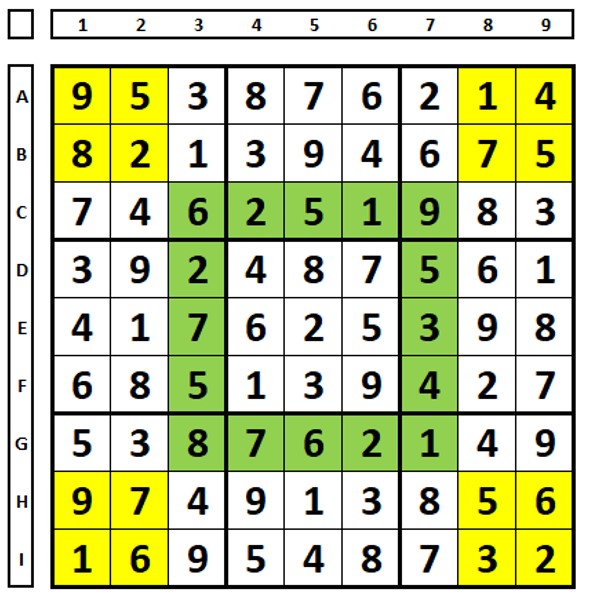
Em que se pode usar a informação dada? Um exemplo.
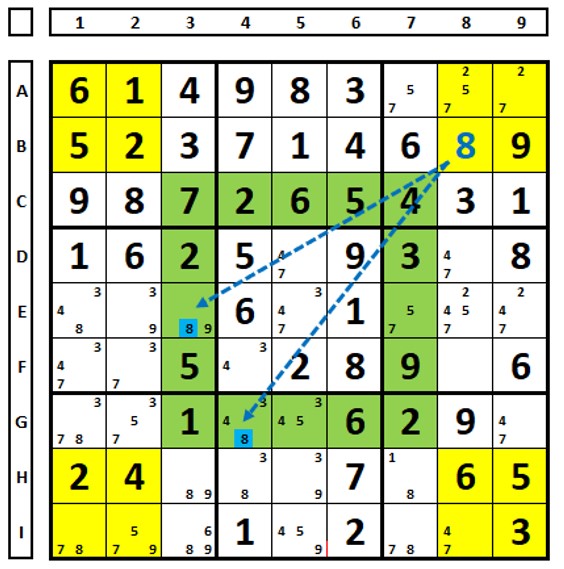
No Sudoku abaixo, o número “8” marcado em azul (célula B8) somente pode estar em uma das células E3 ou G4, ou nas duas (pois, no máximo pode estar também em I1). Logo há um link forte entre estas duas células, como nunca se viu antes neste livro. Vamos tentar um X-Ciclo?
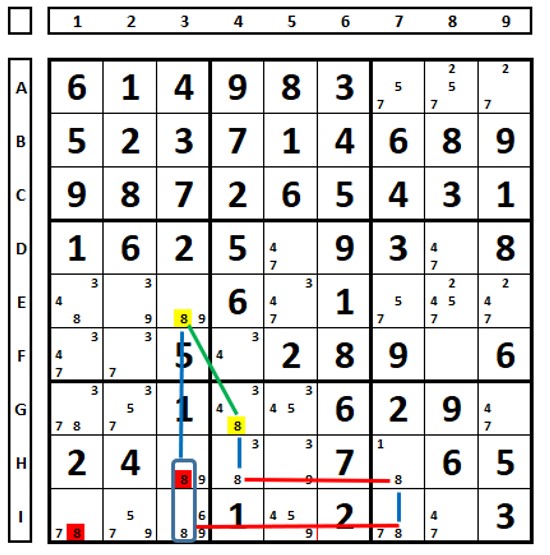
Link em verde (link forte transformado em link fraco). Conhecer a posição dos dois números “8” permitiu a construção deste X-ciclo e as exclusões mostradas. Lembre-se que os números “8” nas células H3 e I1 foram excluídos porque estão na linha dos links vermelhos.
No Sudoku abaixo o número “8” não está nos conjuntos amarelos como pista ou como candidato, logo pode ser excluído das posições marcadas em vermelho.
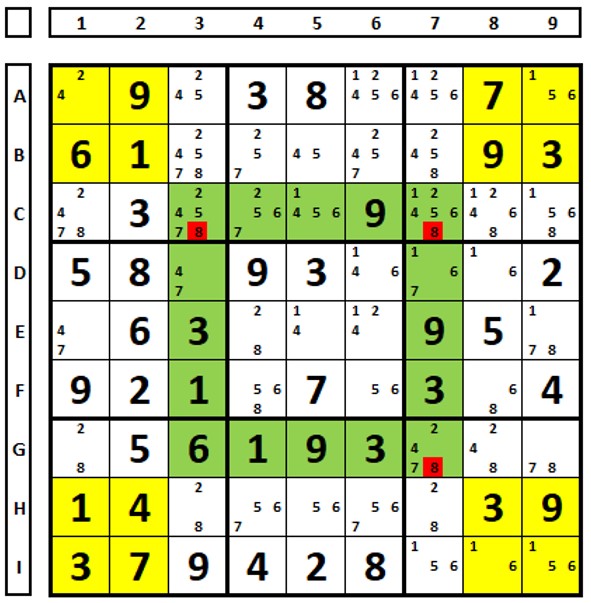
No Sudoku abaixo, há dois números “3” no conjunto verde. No conjunto amarelo haverá um número “3” no conjunto azul e um no conjunto cinza, completando os dois necessários para igualar com o conjunto verde. O número “3” na célula H2 pode ser excluído. Ops, o número “3” na célula B9 também pode ser excluído. É mais fácil ver o X-Wing (A2/A9 com I2/I9) e fazer as exclusões. Como já foi dito, várias técnicas levam a mesma conclusão (em sudokus bem feitos).
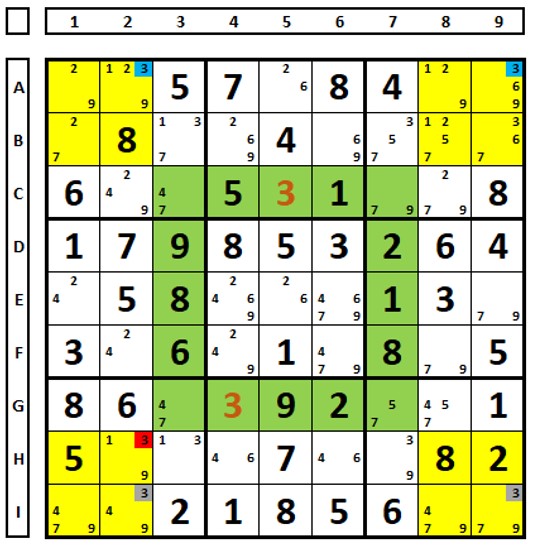
No Sudoku abaixo, há somente o número “2” no conjunto amarelo na célula A8, por consequência somente háverá somente um número “2” no conjunto azul claro. Somente o número “2” na célula D7 ou na célula G4 será solução para o sudoku. Ambas enxergam este número na célula D4, podendo ser ali excluído.
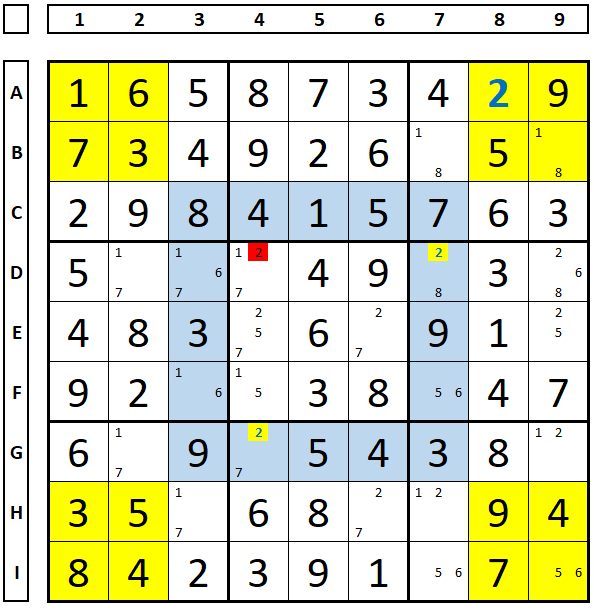
Variante 2
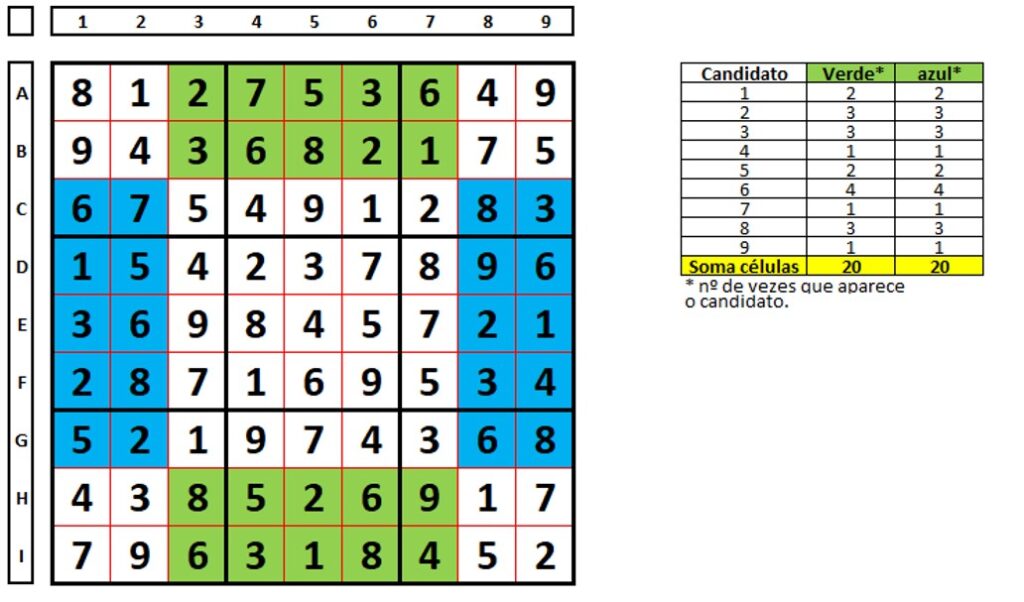
Há o mesmo número (dos mesmos candidatos) nas áreas verdes e azuis. Direto a um exemplo. O conjunto verde tem os mesmos números repetidos por igual no conjunto azul.
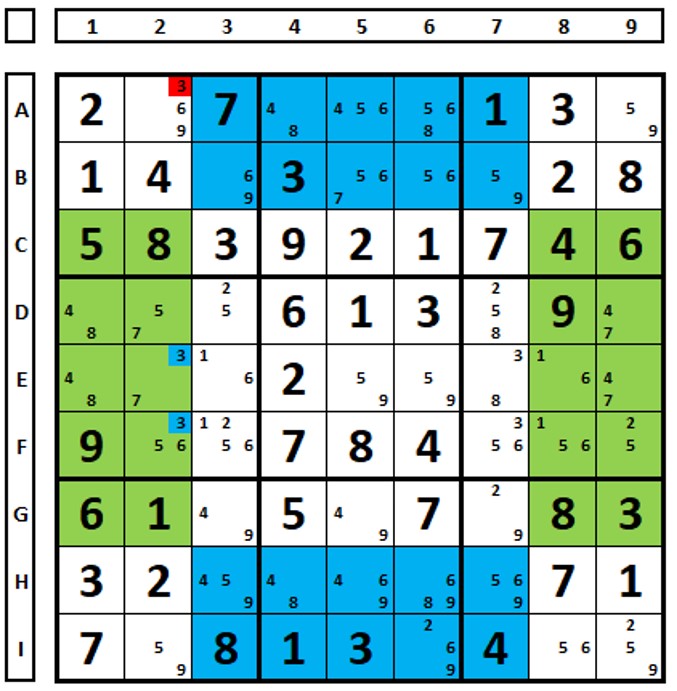
No Sudoku abaixo a região azul possui dois números “3” como única solução neste conjunto (B4 e I5) e não há candidato em nenhuma outra célula azul. Logo, no conjunto verde somente poderá existir dois números “3”. Um já está fixo na célula G9, por consequência somente poderá estar numa das posições marcadas (E2 e F2), podendo ser excluído em A2.
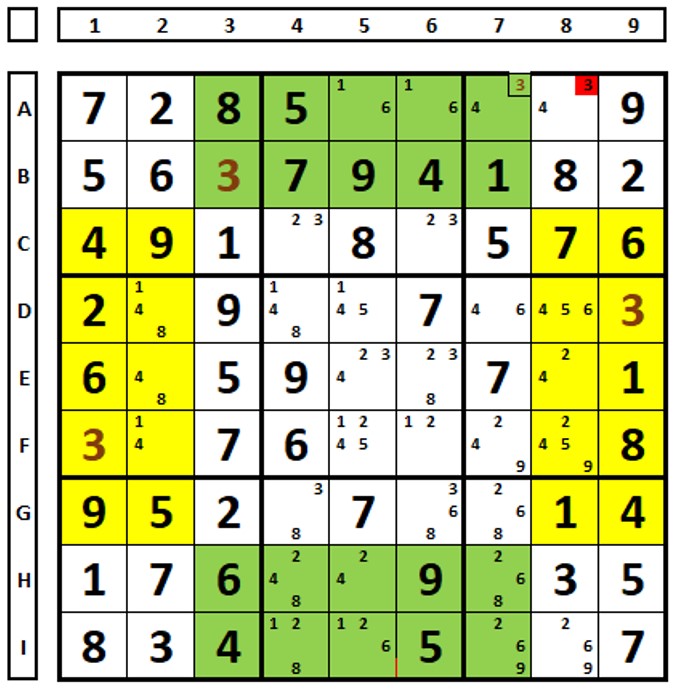
No Sudoku abaixo, no conjunto amarelo o número “3” está nas duas posições marcadas em marrom (são dois). No conjunto verde está na célula B3 e obrigatoriamente na célula A7 (examine coluna 7). O número “3” em A8 pode ser excluído. Lembre-se, várias técnicas podem levar a mesma conclusão, o número “3” na célula H8 faria a mesma exclusão (método do número único).
No Sudoku abaixo, nos conjuntos verdes obrigatoriamente haverá quatro números “3”. Logo, nos conjuntos amarelos haverá quatro números “3”. O número “3” na célula C8 é solução desta célula. Qual o outro métido que chegaria a mesma conclusão?

No Sudoku abaixo, o número “5” está em duas posições no conjunto amarelo como pista (células D1 e F8), podendo estar numa terceira posição (célula C9). Então, obrigatoriamente, há dois números “5” no conjunto verde, podendo haver um terceiro. Mas, ao observar o conjunto verde, só há a possibilidade da colocação de mais um número “5” (além do número “5” na célula B3), ou na linha A ou linha I. Ao olhar o número “5” na célula A4 e colocá-lo como solução do Sudoku, cria-se a seguinte situação:
Conclusão: este número deve ser excluído da célula A4.

No sudoku abaixo o número “4” aparece somente uma vez no conjunto amarelo (uma vez como “pista” na célula E2, e nenhuma vez como candidato nas demais células amarelas). Logo, somente pode aparecer uma vez no conjunto verde (na célula A4), com isto o candidato em H3 deve ser excluído.

No sudoku abaixo o número “7” aparece somente uma vez no conjunto amarelo (na célula I8). Olhando o conjunto verde, a escolha do número “7” na célula C3 faz com que este número seja solução na célula D7, o que contraria a regra (neste caso só pode haver um número “7” no conjunto verde), logo pode ser excluído da célula C3. Isto não significa que os números marcados em vermelho não sejam alguns deles solução do sudoku.