Antes de continuar com técnicas que são um pouco mais complexas, serão vistas algumas possibilidades de testes que poderão ajudar na solução do passatempo.
Em muitas ocasiões pode-se eliminar candidatos (ou descobrir algumas inclusões/exclusões) testando pares conjugados. Não se trata de um método de tentativa e erro, pois o sudoku não será resolvido com esta técnica, apenas serão eliminados candidatos em alguma(s) célula(s).
Exemplo 1:
Examinar o seguinte Sudoku. Não é um X-Wing, mas permite fazer o seguinte teste (verdadeiro/Falso), escolher primeiro a célula C5 e depois a célula C8 como sendo o local correto para alocar o número “6” e a consequência nas demais células do Sudoku.
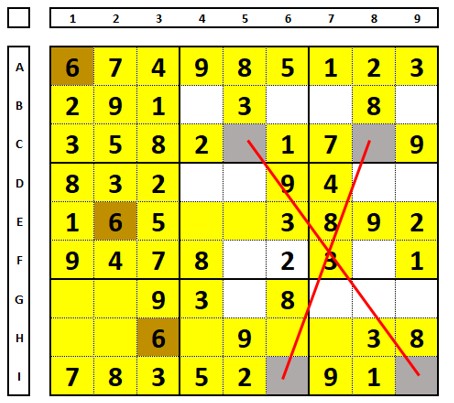
Como se observa, sendo qualquer uma das células (C5 ou C8) corretas para o número “6”, as células B6, D5, D8, G5 e I9 não conterão o número “6”. Em qualquer hipótese a célula I6 contém o número “6”.

Exemplo 2:
No Sudoku abaixo, para qualquer escolha do número “1” como solução na linha D, acarretará a eliminação do número “1” nas células A9 e B9.

Exemplo 3:
Ao examinar os pares formados nas linhas B e F para o número “5” pode-se verificar que, para qualquer escolha na linha B, o número “5” na célula E7 será excluído.

Exemplo 4:
Examinando este Sudoku, onde aparentemente o XY-Wing não permite exclusões em outras células, pois o cruzamento possível é na célula B4 onde já está localizado o número “2”.

Vamos testar o número “6” nas posições que ele poderia ocupar neste XY-Wing pois, para qualquer escolha na célula F3, o número “6” estará na célula B3 ou na célula F4.

Para qualquer escolha, o número “6” da célula C4 pode ser excluído.
Exemplo 5:
Examinar o Sudoku abaixo.

Pode-se escolher como solução o número “8” na coluna 7, na célula D7 ou H7. Testando as duas hipóteses.
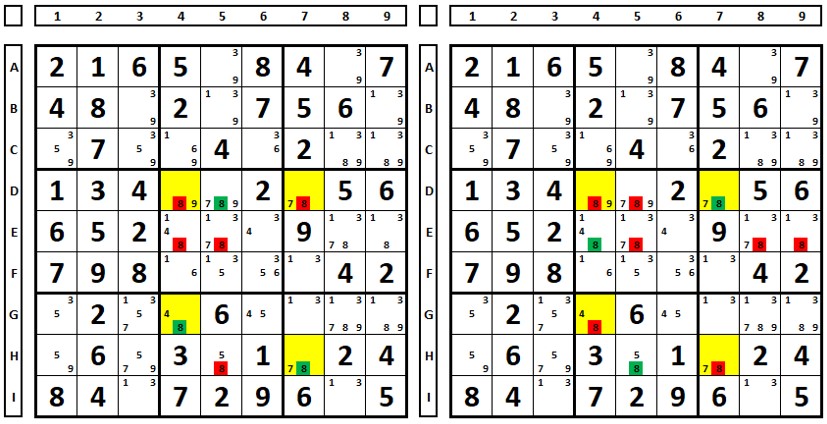
Em qualquer uma das duas hipóteses, o número “8” das células D4 e E5 pode ser excluído.
Exemplo 6:
Examinando o número “3” no Sudoku abaixo:
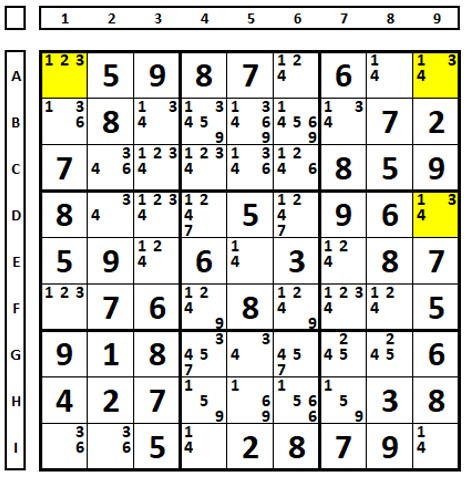
Examinar o resultado da escolha do número “3” na linha A (célula A1).
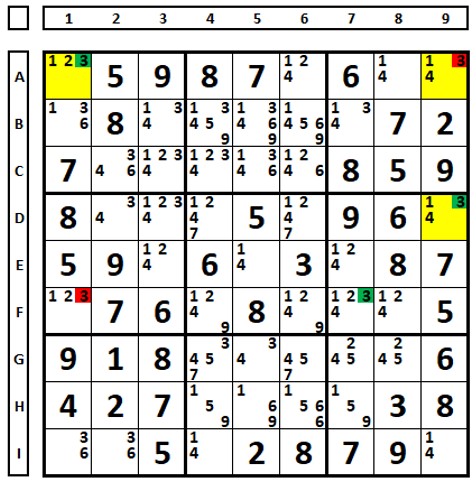
A escolha do número “3” como solução na célula A1 leva ao resultado de dois números “3” “solução” no QM6, o que contraria a regra (somente pode haver um número “3” como solução no QM6). Por consequência, o número “3” solução é o da célula A9.
Exemplo 7:
Pode se descobrir a posição de determinado número ou a impossibilidade deste estar em determinada célula.
Como não é possível que um mesmo número ocupe duas vezes a mesma linha, coluna ou QM, pode-se verificar as possibilidades de localização deste e eliminar a(s) célula(s) não utilizada(s).
As células em branco no Sudoku abaixo mostram as posições possíveis de serem ocupadas pelo número “1”
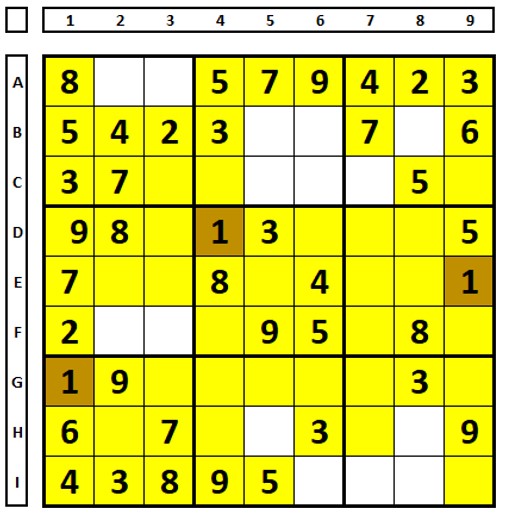
A partir do QM3, onde há duas possibilidades, procurar quais combinações resolveriam este Sudoku. Escolher a célula C7 e testar, depois fazer o mesmo com a célula B8.
É possível encontrar estas três (as posições em verde mostram onde estaria o número “1” solução).
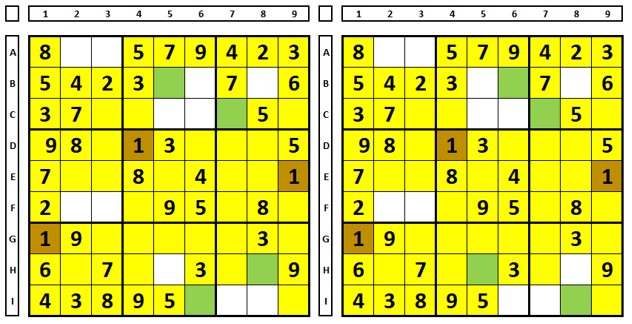
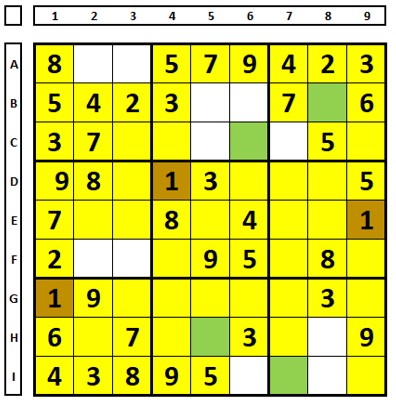
Nenhuma das três possibilidades utiliza a célula C5, logo o número “1” pode ser excluído desta.
Outro exemplo:
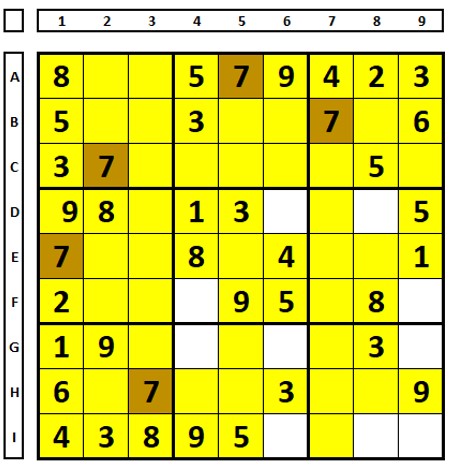
Neste exemplo, as células em branco mostram as possíveis soluções para o número “7”. Estas são as possibilidades de localização, começando no QM5 e usando letras (A e B) em vez de cores
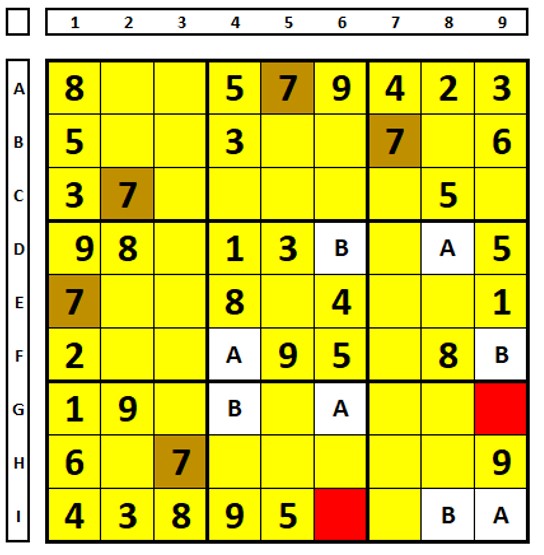
O número “7” pode ser excluído como solução das células marcadas em vermelho, que enxergam A e B (ou cores diferentes, se tivessem sido utilizadas). Se alguma célula contivesse ambas as letras (AB), o número “7” seria solução desta célula.
Este método é chamado Pattern Overlay Method (POM). Uma regra deste método é que a célula que não faça parte do “padrão” (no caso acima A ou B) não contém o número procurado. Não haverá discussão deste método neste site. É recomendável entendê-lo após estar familiarizado com todas as técnicas aqui apresentadas pois são necessárias para resolução de Sudoku por este método, muito “matemático”.
Curioso sobre este método? Veja mais nos links abaixo. Se necessário clique com o botão esquerdo do mouse no site e peça para traduzir para o Português (ou outra língua de sua preferência). Há outros sites, basta consultar.

