As previously seen, a locked set is one that has N cells and N candidates. For example, a Naked Pair. Reviewing an example from the book. In the box below, the cells highlighted in yellow form a Naked Pair or locked set, N (=2) cells with N+0 (=2) possible candidates. That is, two candidates in two cells.
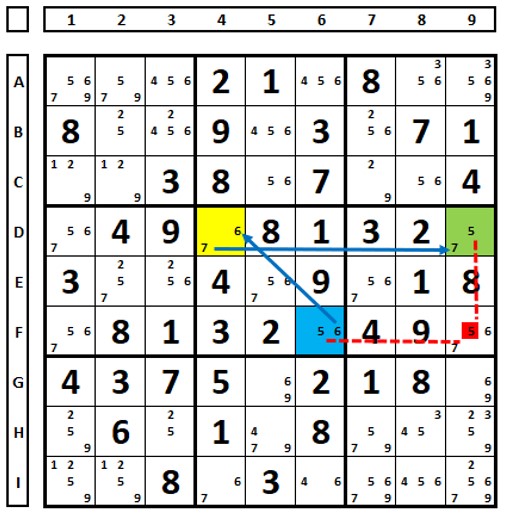
An XY-Wing is an interesting way to demonstrate ALSs, as shown in the example below. In the first ALS highlighted in yellow, two cells (N) contain three numbers (4,5,7) (N+1). In the second ALS highlighted in green, one cell (N) and two numbers (7,5) (N+1). The number “5” in the green ALS “sees” all the “5” numbers in the yellow ALS. The number “7” in red (cell I2) “sees” both “7” numbers in the two ALSs, so it can be excluded. It is easy to demonstrate this in this example just by looking at it. If the number “7” were the solution in I2, there would be two “4” numbers left in box 9 (in H7 and I9), which violates the rule (two equal numbers in the same box).

Retaking an example of XYZ-Wing previously seen. The example was left – the colored one – in the form of XYZ-Wing. Where are the ALSs? In the set D3/F2, there is an N+1 (two cells and three possibilities: (1,4,6)). The other ALS is the cell A2 where there is an N+1 (one cell and two possibilities). The number “1” in A2 “sees” all the numbers “1” in the second set (D3/F2). The number “6” in E2 can be excluded because it “sees” all the numbers “6” in the two sets.
Given the examples, the rule is that a number (x) is common to both ALSs and this number sees all the same numbers (x) in the other set. Both ALSs have a number (y) common to both, but which does not fully see each other. The numbers (y) in the cells that are outside of the ALSs, but which see the numbers (y) in both ALSs, can be excluded.
The “x” is also called a Common Candidate Restriction (CCR). It is a solution in one ALS or the other.
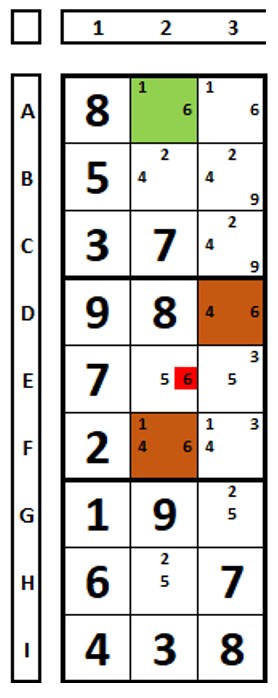
In the same example above, now in ALS form (below). The number “1” (our “x”) in the green ALS sees all the “1” numbers in the brown ALS. The number “1” is common to both ALSs. The number “6” (our “y”) is common to both ALSs, but the “6” number in the green ALS does not see all the “6” numbers in the brown ALS (in D3). The “6” number in cell E2 sees all the “6” numbers in both sets and can be excluded from this cell.
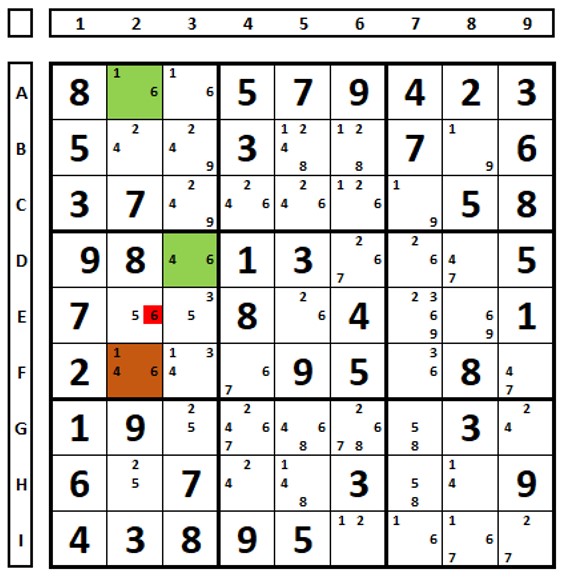
Carefully examine the usefulness of the Restricted Common Candidate (RCC). In the Sudoku below, either the number “1” is the solution in the green ALS or in the brown ALS. If it is in the green, the number “1” in F2 is excluded, and we would have a Naked Pair in D3/F2 (4,6), which would then exclude the number “6” in E2. If the number “1” were the solution in the brown ALS, the number “1” would be excluded in the green ALS, leaving the number “6” in A2, which would also exclude the number “6” in E2.
Note that the WXYZ-Wings below are also ALSs
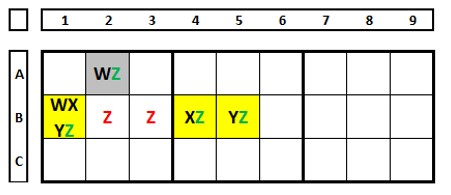
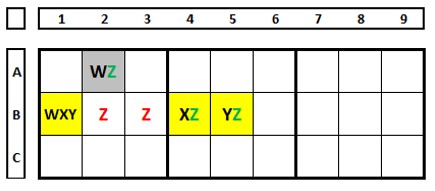
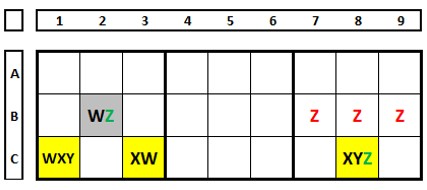
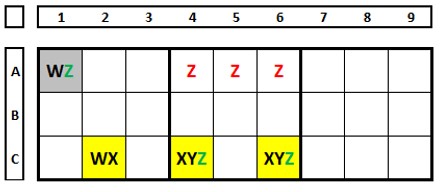
In the Sudoku below, there are two ALSs, one in blue and one in yellow, both N+1. The number “1” in both sets sees each other, the number “4”, common to both but not restricted, allows to exclude the number “4” in B4. And with this, quickly solve this sudoku. Do the nine’s check, choose the number “4” as the solution in B4, and see what happens in column 5 of box 5.
In the sudoku below there is ALS marked in yellow and in green. The number “7” is RCC on both. The number “9” in cell C7 sees all the numbers “9” from both ALSs and can be deleted.
The ALS with a single link are the models that were demonstrated above.
ALSs can overlap in all ALS techniques. There is only one restriction: the overlapping area between two ALSs should not contain a CCR (Common Candidate Restriction).
ALS with double linkage. (ALS – XY)
When two ALS share common restricted numbers, that is, each one will be a solution in one or the other, the cells that see these numbers can have these numbers excluded.
Showing a simple example below. In the Sudoku below, a Naked Triple was transformed into two ALSs. A pink one (N+1) and a green one (N+1). The numbers (4,6) in the green ALS see all the numbers (4,6) in the pink ALS. But there is no third common number that allows them to be eliminated in other cells outside of the ALSs. However, since there is dependence between them (as in the Naked Triple), the number “4” can be excluded in F9.
In the sudoku below are two ALSs in green to yellow, with the numbers “2” and “5” as Restricted Commons.
What happens when you choose a Restricted Common as a solution? If we choose the number “2” in cell B6, the yellow set is blocked with four cells and four numbers (1,4,5,6). When choosing the number “5” in cell C8 there is also a block in the yellow set. When inverting the choice using the yellow set, the same blocking occurs in the green set.
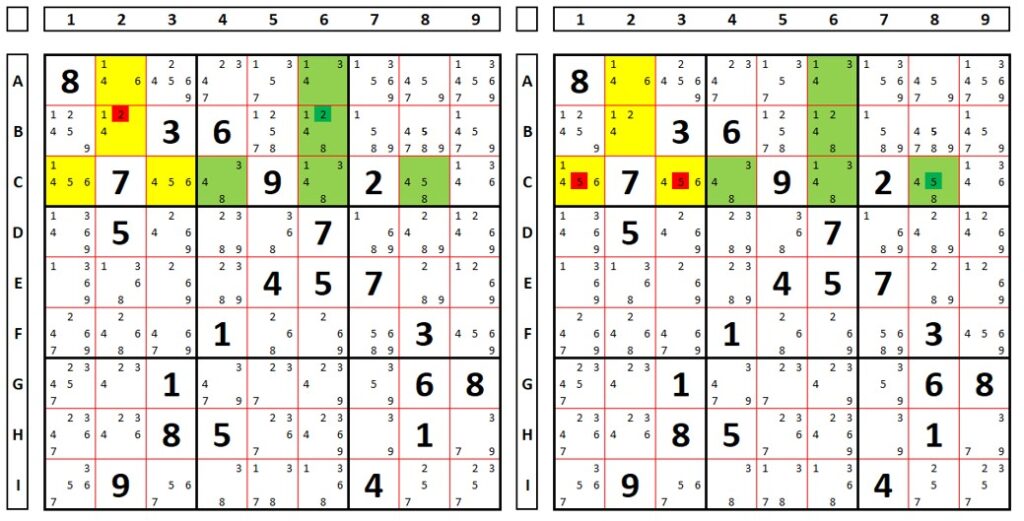
What’s the consequence? All numbers that see all RCCs from both sets can be deleted, as well as those that see Restricted non-Commons in Unity.
The number “2” in cell B1 can be excluded as it sees the two numbers “2” (which are RCCs) in the two ALSs.
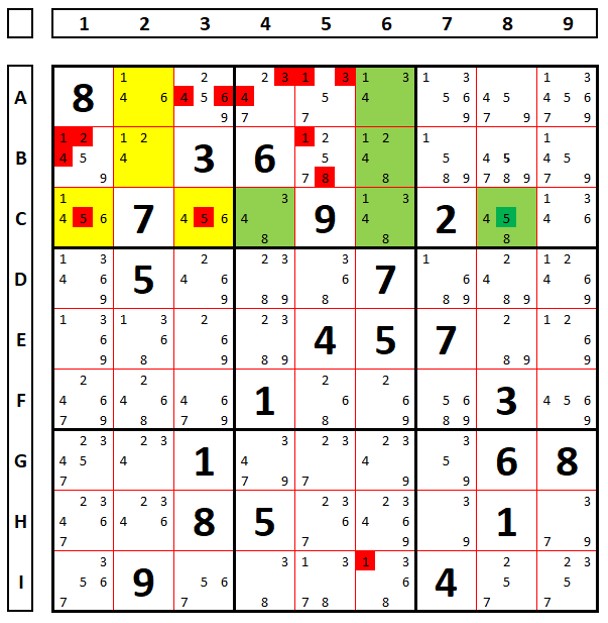
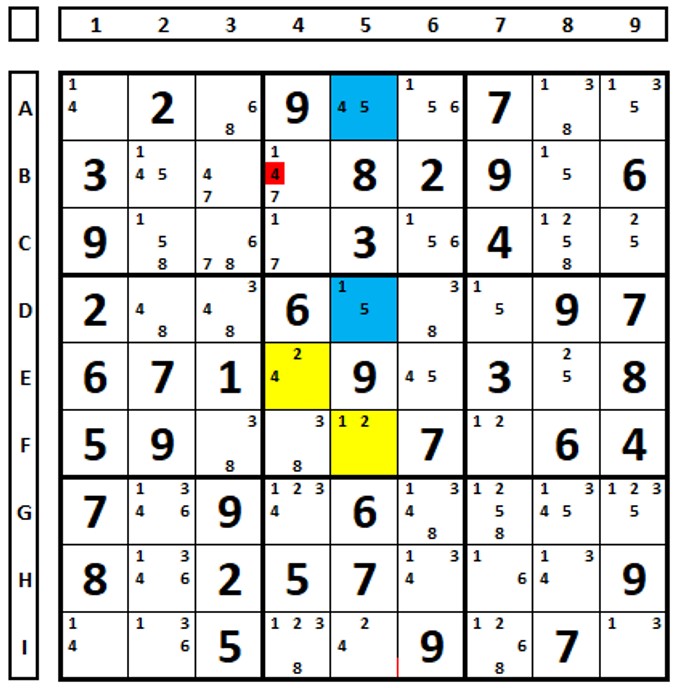
In the Sudoku below there are two ALSs (yellow and blue sets) and the numbers “7” and “9” are common and restricted to both. The number “9” in cell G2, which sees all the “9” numbers in both sets, can be excluded.
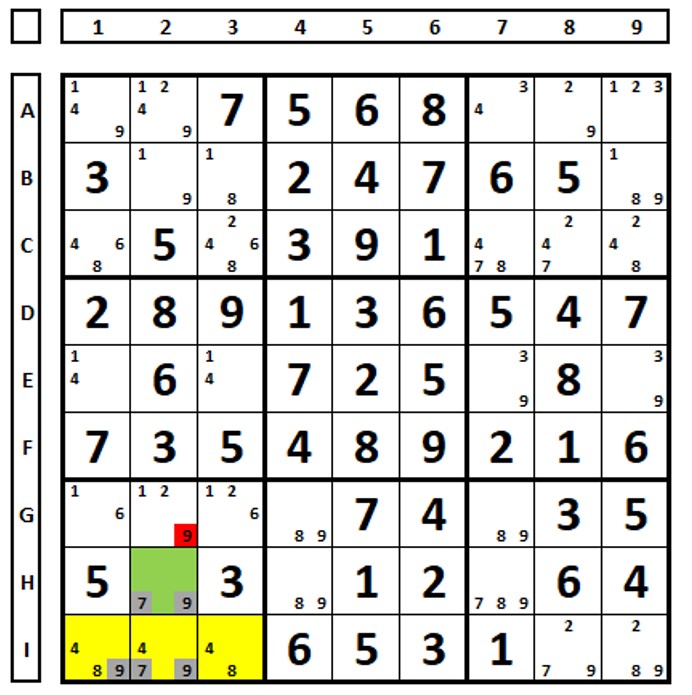
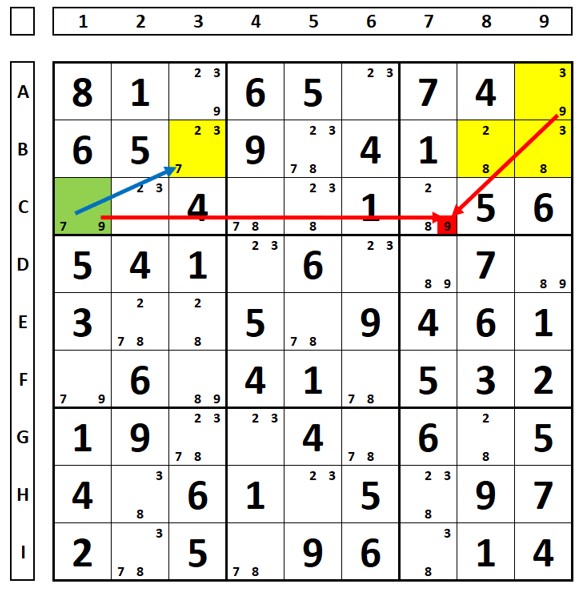
In the sudoku puzzle below there are the two ALSs marked in yellow and green, with the numbers “3” and “9” marked as RCC. The number “7” in cell C3 sees all the “7” numbers in the green ALS and can be deleted.
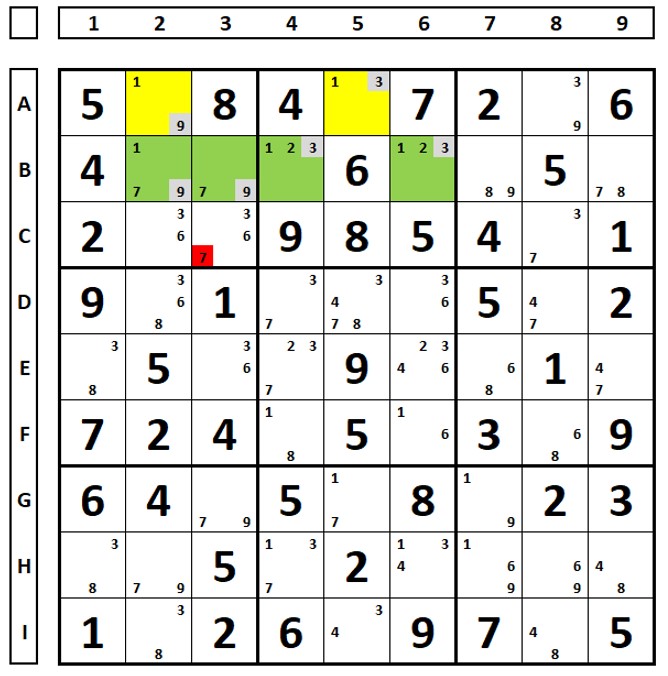
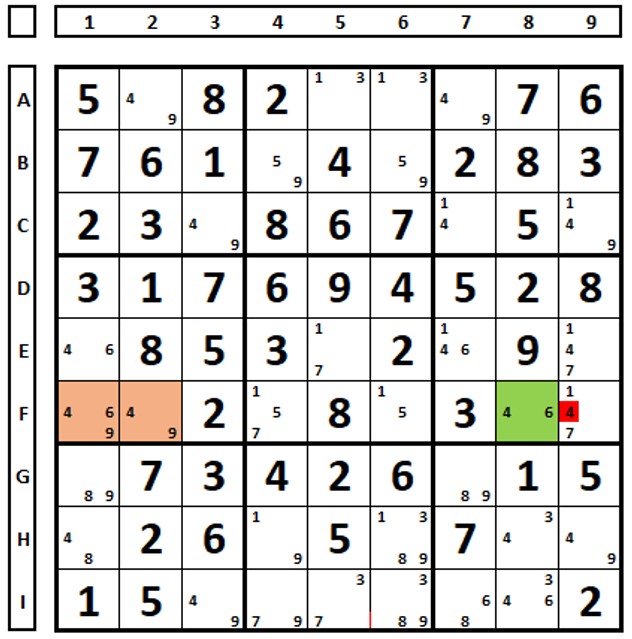
The sudoku puzzle below shows all possible elimination rules with the double-bind ALS. The RCC common to both are the numbers “3” and “8”, with this the numbers “3” in cells E4 and E6 can be excluded as they see the RCC of the two ALSs. The number “3” from cell D2 can be deleted as it sees all the numbers “3” from both ALSs. The number “6” in cell E6 can be deleted as it sees all of the green ALSs.
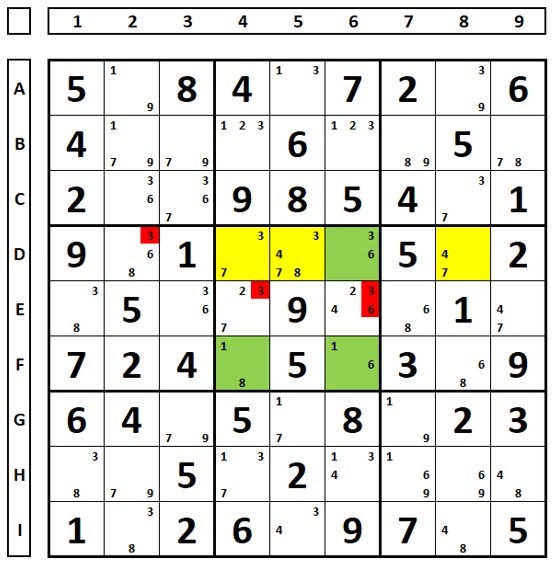
In the same sudoku, the RCC of the two ALSs are the numbers “3” and “9”. The “1” numbers marked in red can be excluded as they see “all” the “1” numbers of the yellow ALS.
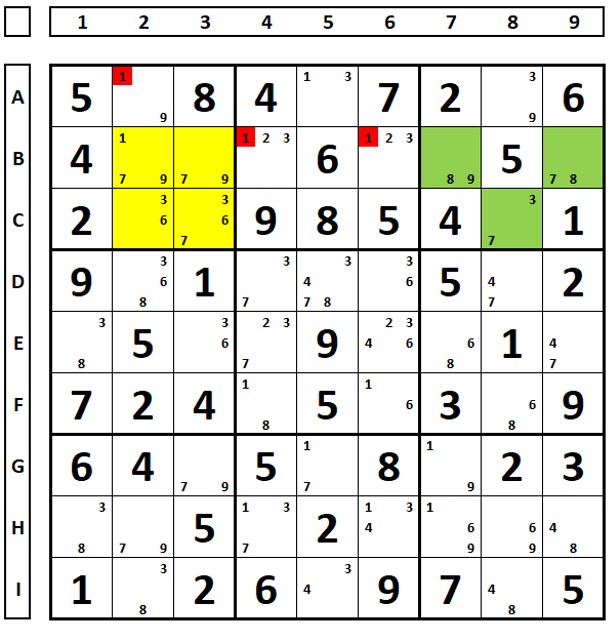
ALS-XY-Wing
Three ALSs are needed, connected together by restricted common numbers, but not the same, where the tweezers tips see a common number, but not the restricted commons.
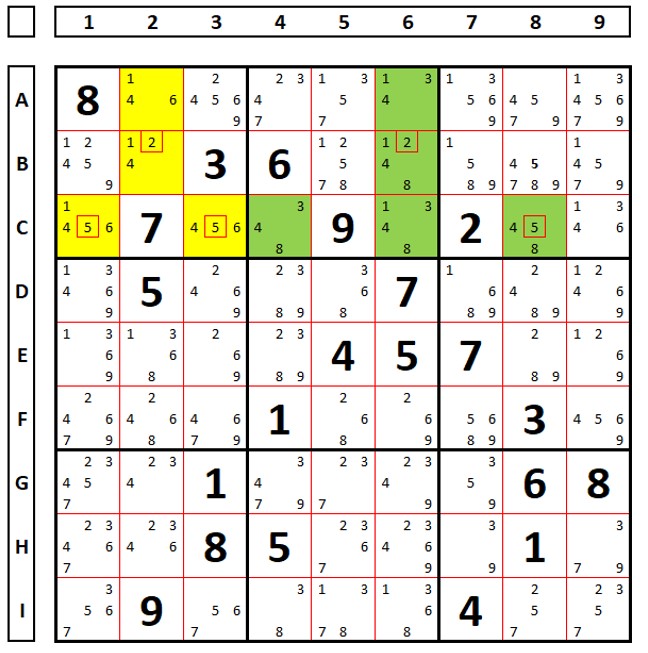
In the Sudoku below there are three ALS (yellow, blue and green). The blue and green ALS have the number “6” as restricted common (RCC). The blue and yellow ALS have the number “8” as RCC. In cell E5 the number “7” sees all the numbers “7” from the green and yellow ALS, so it can be deleted.
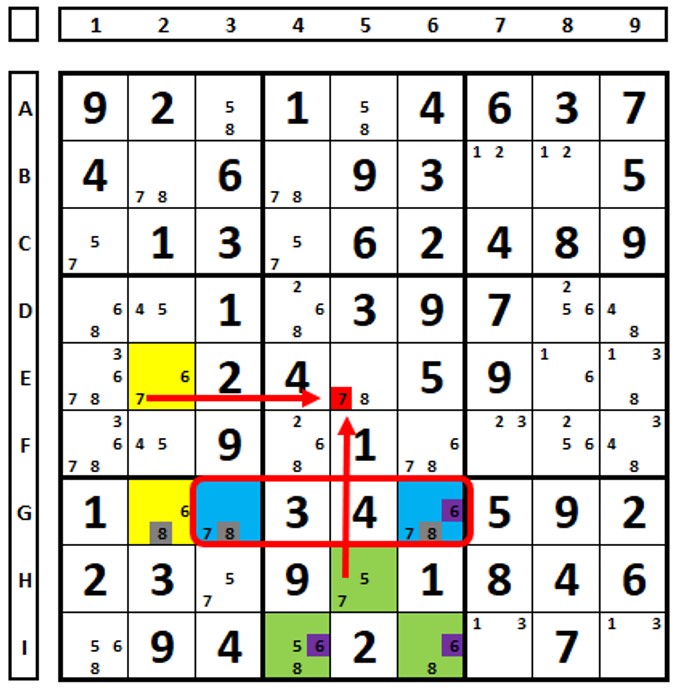
In the Sudoku below, in the XY-WING technique, any choice in the yellow cell leads to the number “5” in the blue or green cell, excluding the number “5” in cell F9.
In the ALS-XY-Wing technique there are three ALS (green, blue and yellow). The number “6” in F6 is common constrained with the same number in D4. The number “7” in D4 is common restricted with the same number in D9. The number “5” in F9 can be deleted, as it sees both numbers “5” at the end of the chain (blue and green cells).