Here we will use the concept of ‘seeing’. This strategy was initially developed with the rule:
Any two cells aligned in a row or column within the same box cannot duplicate the contents of any bi-value cell that both cells see.
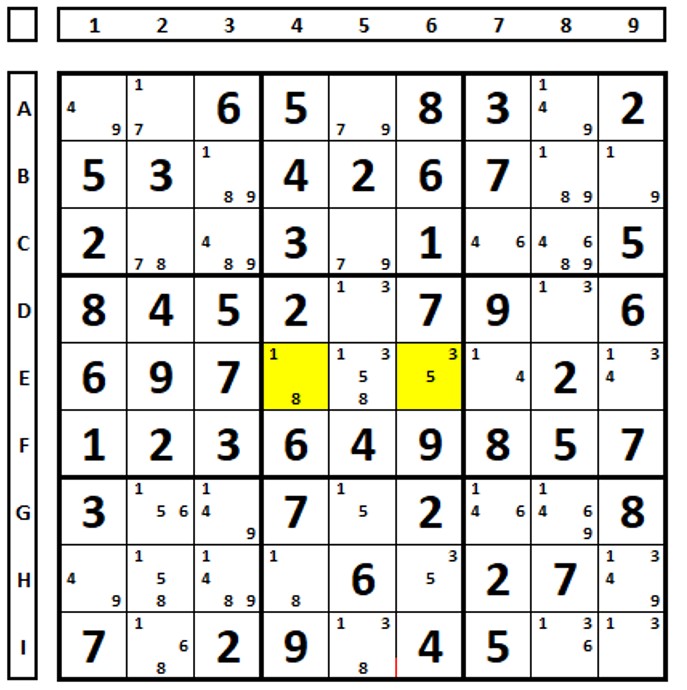
Example in this partial sudoku, examining row B. Row B, as well as the cells marked in yellow, was chosen because the combination of the number ‘6’ (B7) and the number ‘1’ (B9) leaves cell B1 unsolved (blank). Examining the consequences in this partial sudoku.

Below is a table with the consequences of choosing the possible combinations between B7 and B9. The combination 2(B7) and 1(B9) leaves the number “7” as a solution in cells B4 and B6, but there can’t be two identical numbers in a unit (row or box in this case), which excludes this possibility.
The same goes for option 5(B7) and 1(B9), with “6” in B1 and 6(C2) both in the same box.
Option 5(B7) and 5(B9) also excludes this option.
Option 6(B7) and 1(B9) leaves cell A8 blank. Options 2(B7) and 5(B9) and options 6(B7) and 5(B9) are valid, but both contain the number “5” as a solution to cell B9.
Conclusion: the number “5” is a solution in cell B9.

But the technique can be extended, as in the partial sudoku below. The three cells in yellow were chosen to see the possible combinations.
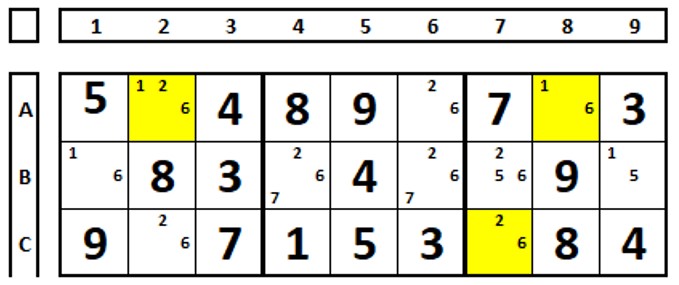
The possibilities for combinations between the three cells are shown in the columns A2, A8, and C7 below. The yellow cells show the rule violations of Sudoku (in the same UNIT, there cannot be two identical numbers, a cell cannot be left blank, and a unit must have all numbers from “1” to “9”). Try to make the table. The blank rows show the possible combination options for the three cells. In all of them, B1 = 1 and B9 = 5, so these values are the solutions for these cells.
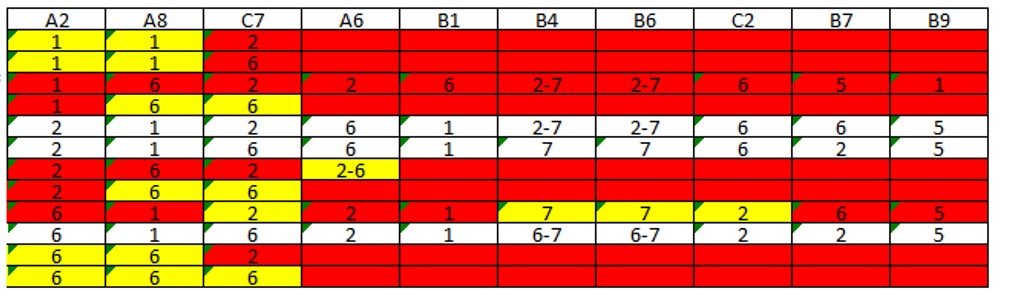
Do the exclusions carefully, often when examining a possibility, you may have associated an XY-Wing, an X-wing, a Singularity, among others, which allow expanding the possibilities of inclusion/exclusion.
One last example. Observe box 5 and box 7. There are the numbers “1”, “3”, “5”, and “8”. Building a table with the two cells marked in yellow: