Before moving on to techniques that are a bit more complex, we will look at some testing possibilities that can help solve the puzzle. In many occasions, numbers can be eliminated (or some inclusions/exclusions discovered) by testing conjugate pairs. This is not a trial and error method, as the Sudoku will not be solved with this technique, only candidates will be eliminated in some cell(s).
Example 1:
Examine the following Sudoku. It is not an X-Wing, but it allows for the following test (true/false): choose first cell C5 and then cell C8 as the correct location to place the number “6” and observe the consequences in the other cells of the Sudoku.
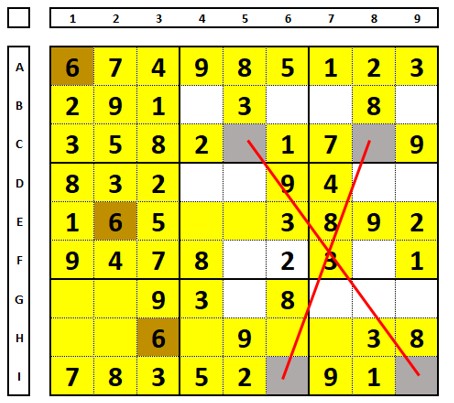
As you can see, if either of the cells (C5 or C8) is correct for the number “6”, the cells B6, D5, D8, G5, and I9 will not contain the number “6”. In any case, the cell I6 contains the number “6”.

Example 2:
In the Sudoku grid below, for any choice of the number “1” as a solution in row D, it will result in the elimination of the number “1” in cells A9 and B9.

Example 3:
By examining the pairs formed in rows B and F for the number “5”, it can be verified that for any choice in row B, the number “5” in cell E7 will be excluded..

Example 4:
Examining this Sudoku, where apparently the “L”, XY-Wing, does not allow exclusions in other cells because the possible intersection is in cell B4, where the number “6” could be excluded if it were there, but the number “2” is already located there.

Let’s test the number “6” in the positions it could occupy in this XY-Wing because, for any choice in cell F3, the number “6” will be in either cell B3 or cell F4:

For any choice, the number “6” in cell C4 can be excluded.
Example 5:
Examine the Sudoku below:

You can choose the number “8” as a solution in column 7, in either cell D7 or H7. Testing both hypotheses:
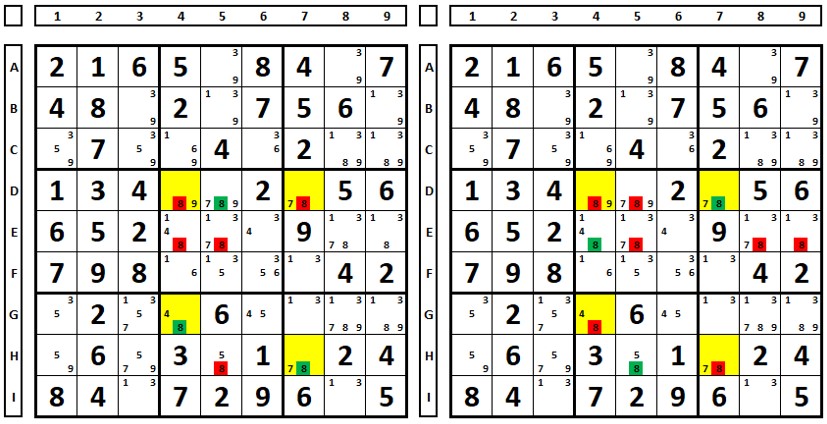
In either case, the number “8” in cells D4 and E5 can be excluded.
Example 6:
Examining the number “3” in the Sudoku below:
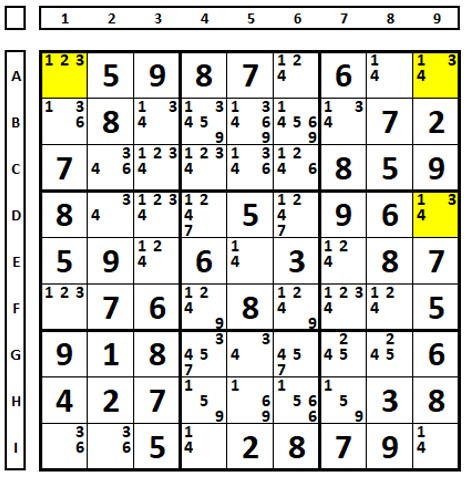
Examine the result of choosing the number “3” in row A:
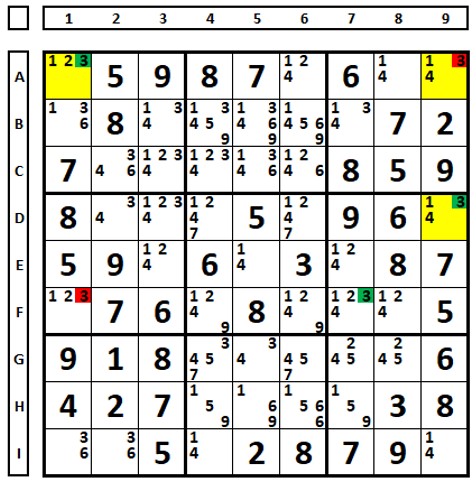
Choosing the number “3” as the solution in cell A1 leads to the result of two “3” “solution” numbers in box 6, which violates the rule (there can only be one “3” as a solution in box 6). Consequently, the solution “3” number is in cell A9.
Example 7:
You can discover the position of a certain number or the impossibility of it being in a certain cell.
As it is not possible for the same number to occupy the same line, column or QM twice, you can check the possibilities of locating this number and eliminate the unused cell(s).
The blank cells in Sudoku below show the possible positions to be occupied by the number “1”
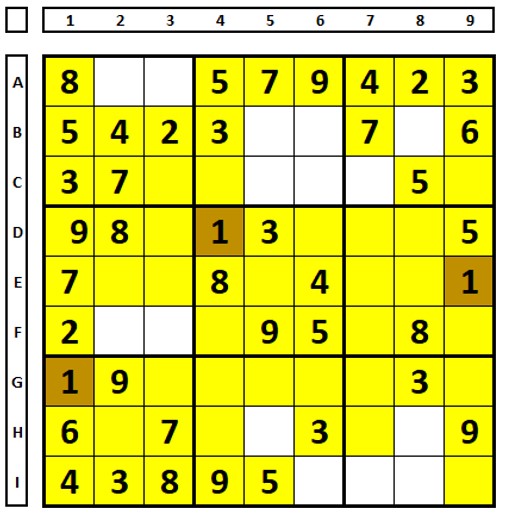
Starting from box 3, where there are two possibilities, look for which combinations would solve this Sudoku. Choose cell C7 and test, then do the same with cell B8.
It is possible to find these three (the positions in green show where the number “1” solution would be).
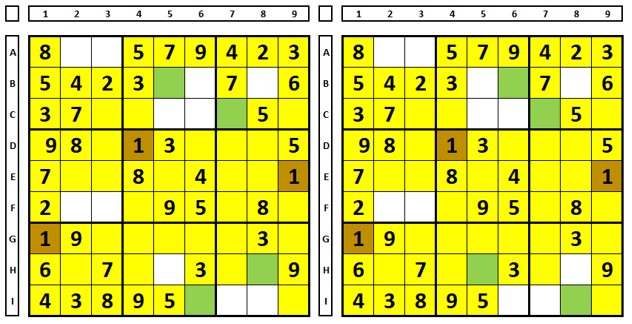
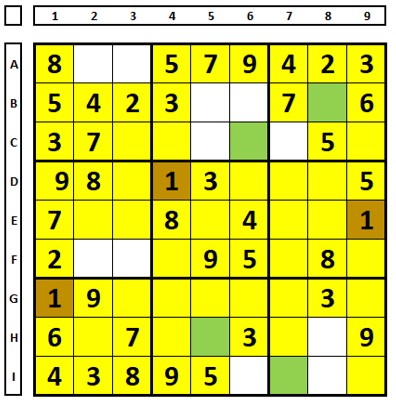
None of the three possibilities uses cell C5, so the number “1” can be excluded from it.
Another example:
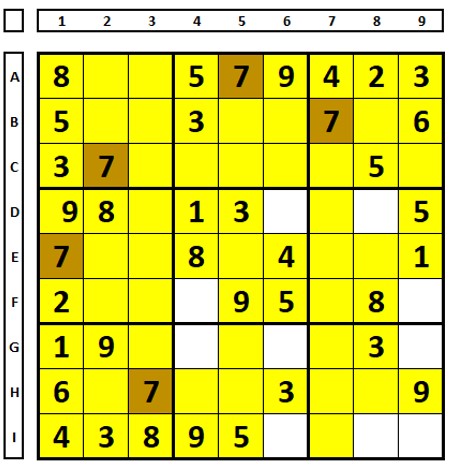
In this example, the blank cells show the possible solutions for the number “7”. These are the localization possibilities, starting from QM5 and using letters (A and B) instead of colors
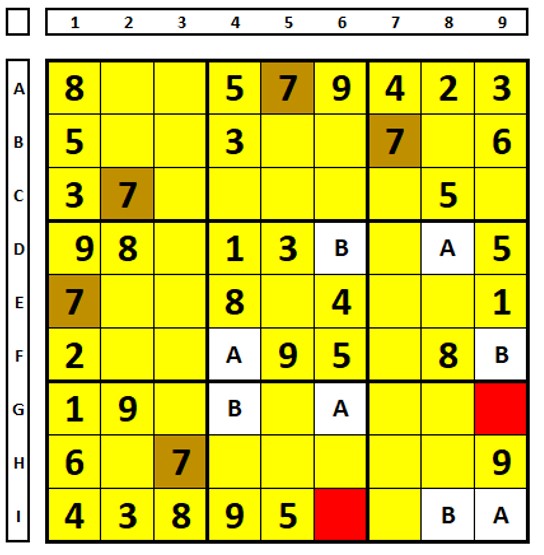
The number “7” can be excluded as a solution for cells marked in red, which see A and B (or different colors, if they had been used). If any cell contained both letters (AB), the number “7” would be the solution for that cell.
This method is called Pattern Overlay Method (POM). A rule of this method is that the cell that is not part of the “pattern” (in the above case A or B) does not contain the number sought. There will be no discussion of this method on this site. It is recommended to understand it after becoming familiar with all the techniques presented here, as they are necessary for solving Sudoku using this method, which is very “mathematical”.
Curious about this method? See more in the links below. If necessary, click with the left mouse button on the site and ask it to be translated into Portuguese (or another language of your choice). There are other sites, just check.

