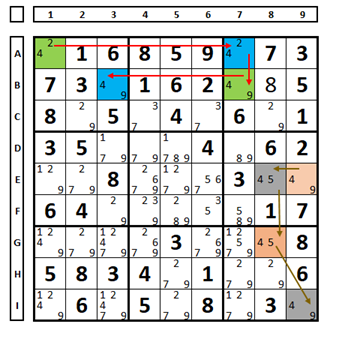
Used when there are two sets of colors in a Sudoku. In the Sudoku below, for the number “4”, there is a green/blue set shown by the red arrows and a gray/pink set shown by the brown arrows.
Eliminating one set of colors:
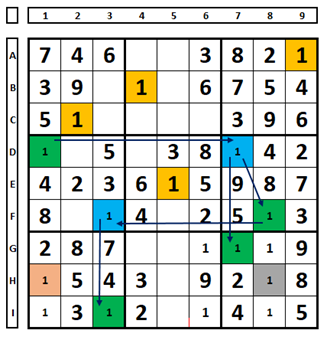
In the example below, for the number “1”, there is a set (green/blue), which started in cell D1 and followed through the conjugate pairs formed in each UNIT. There is another set (pink/gray) in the H row, and one of the cells contains the number “1” as the solution to the Sudoku. For any cell chosen as the correct answer in the (pink/gray) set, the green color will be eliminated from the other set, so the blue corresponds to the correct answer for this Sudoku. The numbers “1” in the green cells can be excluded. Complete solving this Sudoku.
Another example, for any choice of the number “4” in the pink/gray set, the cells in green will be eliminated, and the number “4” in the blue cell (A4) is the solution for this Sudoku.
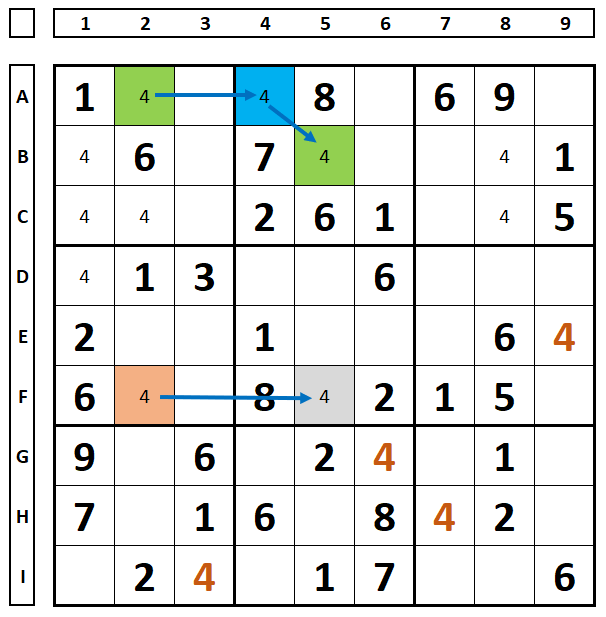
Whenever the two colors of a color set (in this example, pink/gray) see the same color in the other set (green/blue), this color (green) can be eliminated.
Examples of exclusions that can be observed:
Eliminating a series.
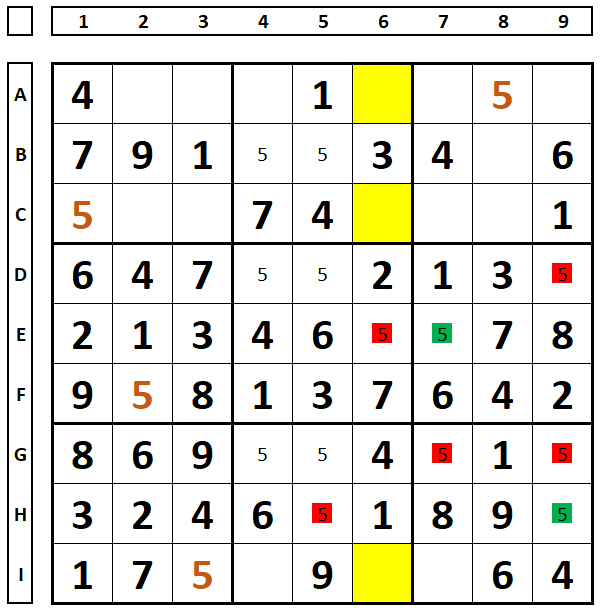
In the Sudoku below, there are two series (green/blue) and (pink/gray) for the number “5”. If the number “5” were a solution in A2 (green), “pink” would not be a solution in box 1 (C1). With the choice of the number “5” in A2, observe that in box 4 the solution would be in E1, which would eliminate “gray” in E6. Since pink or gray is the solution, the number “5” can be excluded in A2. And the blue series contains part of the Sudoku solution.
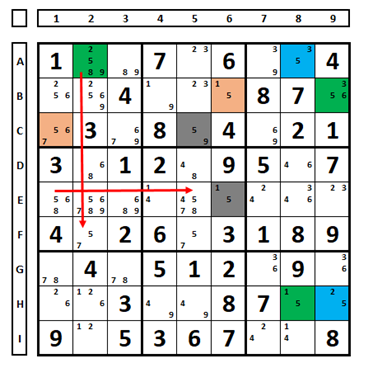
Another example, two series, green/blue and pink/grey. You can choose the pink or gray cell as true, the number “5” in cell H2 will be excluded.

Working better the example above. The pink cell (B4) and the blue cell (C5) in box 2 cannot be Sudoku solutions at the same time. Which forces the green or gray cells to be both Sudoku solutions or at least one. With this, the cells that see the green and gray cells can have the number that sees both excluded (in this case the number “5” in cell H2). Simulate the solutions, always the number “5” in cell H2 will be excluded.
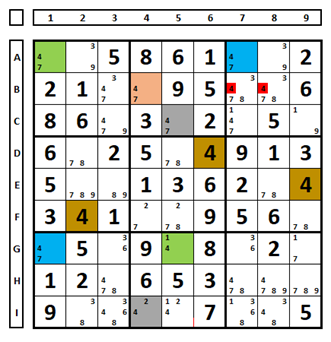
In the example below, for the number “4”. In box 8, the “green” and “gray” cells cannot be Sudoku solutions at the same time, but one will be. As a consequence, cells that see the opposite colors (either “pink” or “blue” will be the Sudoku solution) may have the number “4” excluded.
Using three sets of colors:
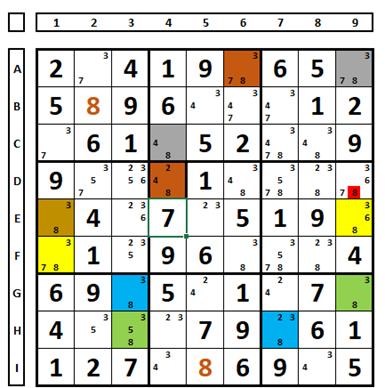
In the Sudoku below, there are three series for the number “8”: blue and green (G3, H3, G9, H7), yellow and brown (E1, F1, E9), and gray and brick (A6, A9, C3, D4). In column 9, all three series are visible and cannot all be a solution to the Sudoku (either one or none). If none of them is a solution, the solution for the Sudoku would be the number “8” in D9, and in this case, the numbers “8” in cells (D4/A9) of the gray/brick series would be eliminated. As one of the two is a solution to the Sudoku, the number “8” can be excluded in D9.
Many times when trying to solve Sudoku using a certain technique, it doesn't work, so check if there are no other conclusions to be drawn, let's call this "extra-technical tip"
Eliminating a cell:
Looking at the number “5”. There are two series, green/blue starting in cell D9 and pink/gray, starting in cell H5.
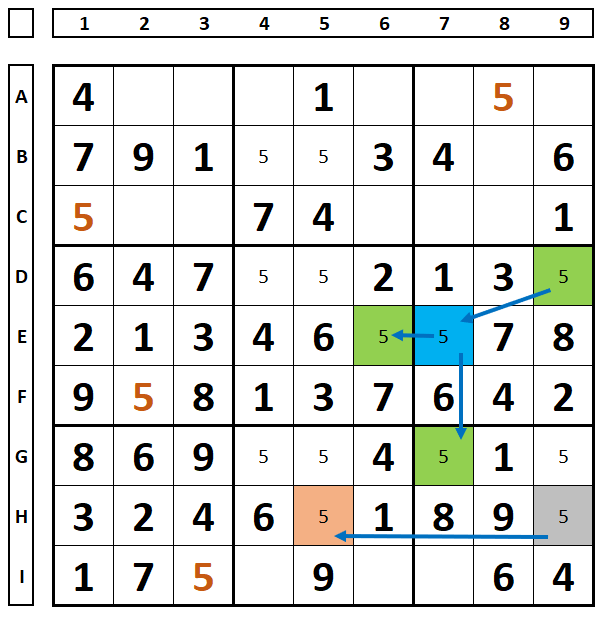
There are no conclusions possible with the multicolor technique. But, if the gray cell is chosen as the correct location of the number “5” (it was marked in green and the exclusions in red), the Sudoku would be unsolved, see figure below, there would be no number “5” in column 6. Therefore, the number “5” from cell H9 can be deleted.