Importante:
Durante o curso, memorize a técnica em que parou. Reinicie o curso na página inicial, clicando na última técnica aprendida.
O que é o passatempo Sudoku?
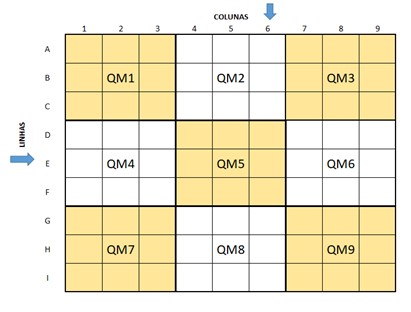
É um jogo de lógica, onde são inseridos os números de 1 a 9 (sem repeti-los), em cada linha e coluna de um quadrado (maior) formado por 9 linhas e 9 colunas. Além de não se repetirem em cada linha ou coluna os números também não se repetem no mesmo quadrado (menor). Os quadrados menores são formados por 3 linhas e 3 colunas.
Há variações no formato quadrado (9×9), podendo ter a forma retangular ou outra figura geométrica. Há também os que tem outras formatações como 12×12. Mas as técnicas aqui descritas podem ser utilizadas/adaptadas para estas novas formas.
Leia a definição novamente, é essencial entendê-la para a resolução de qualquer Sudoku.
O Sudoku é formado por:
Conceito de “pista” e “marcação de lápis = candidatos”
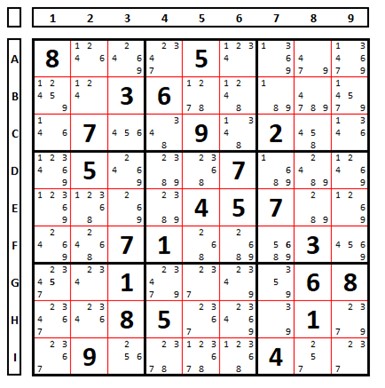
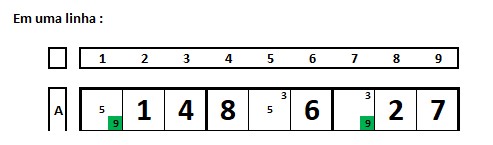
Pistas são os números que orientam inicialmente um Sudoku. Dado o Sudoku abaixo, os números em negrito são pistas (formação inicial do Sudoku) e os vários números menores em cada célula são os possíveis números que podem ocupar estas células que se denominam marcação de lápis ou candidatos.
Conceito de “enxergar”:
Uma célula “enxerga” outra quando estão na mesma linha, mesma coluna ou mesmo QM.
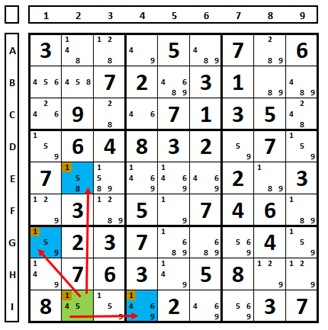
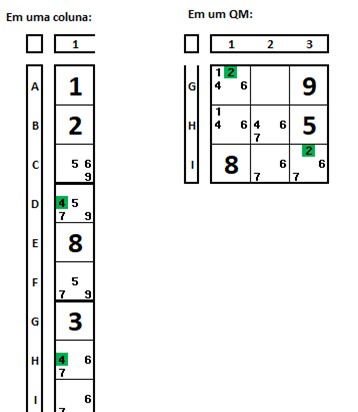
No seguinte Sudoku, o número “1” da célula I2 (marcada em verde) “enxerga” o número “1” nas células marcadas em azul, E2 (mesma coluna), I4 (mesma linha) e G1 (mesmo QM). Para ficar claro, enxerga também a célula H1, A2 e I3 (que contém o número 1).
Este conceito de “enxergar” também serve para números diferentes, em algumas técnicas, mas o conceito é o mesmo (L, C ou QM). Por exemplo, a célula I2 está “enxergando” a célula I7, mesmo que esta não contenha o número “1”, porque estão na mesma linha.
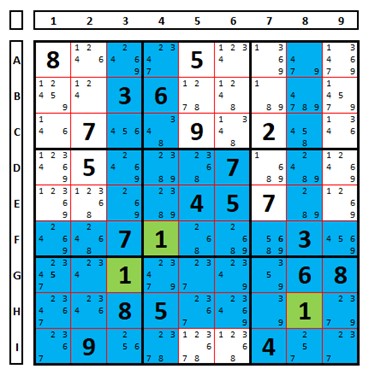
Ampliando o conceito, cada célula “enxerga” todas as outras 8 células de seu QM, bem como todas as outras 8 células da linha e coluna onde se encontra. A célula C7 (marcada em verde) “enxerga” todas as células marcadas em azul. E são posições (as células azuis) onde, pela regra, não haverá o número “2”.
O conceito é importante, pois nos mostra as possíveis posições de um determinado número, como o número “1” no exemplo abaixo, que estará em algumas das células “brancas”, a exceção das pistas dadas (por exemplo, o número “8” na célula A1 é uma pista e o número “1” não pode ocupar essa célula).

Pares conjugados:
Pares de candidatos “únicos” em uma unidade. Na linha A o número “9” encontra-se somente nas células A1 e A7.
Solução única:
Os Sudoku devem ter solução única. Os que permitem mais de uma solução são mal elaborados (inclusive as técnicas de resolução apresentadas neste ou em outros livros ou sites podem apresentar erros nestes sudoku). Mas, felizmente, são difíceis de serem encontrados em publicações de qualidade.
Conceito de UNIDADE:
Neste livro, a palavra UNIDADE se refere a uma coluna, uma linha ou a um QM.
Conceito de Cadeia:
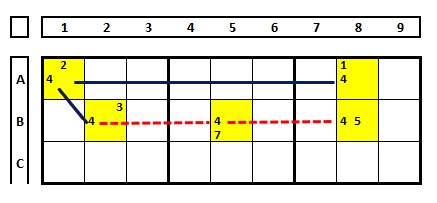
Uma cadeia – ou corrente – é uma relação que se pode fazer entre os números que compõem as células. Ou, são links que saltam de uma célula para outra seguindo certas regras. No exemplo abaixo há uma relação entre as células bi-valor (2/4) que compõem este Sudoku. Quando um número (2 ou 4) for solução em uma célula solucionará o valor em todas as outras células da corrente.
No caso abaixo, nesta corrente as células H2 e E8 são as pontas (o início e final da corrente).

Célula bi-valor são células com dois candidatos onde um dos dois “candidatos” será solução para esta célula. Por exemplo, célula A1, ou o número “2” ou o número “4” será solução do Sudoku
Pode haver mais de uma corrente em um Sudoku. As implicações disto serão mostradas nas técnicas adiante.
Os próximos conceitos serão vistos com detalhes quando técnicas os utilizarem. Leia-os sem preocupação neste momento.
Conceito de links:
Links fortes:
Quando dentro de uma UNIDADE houver a relação: se A então não B ou vice-versa.
No exemplo abaixo são links fortes A1/A8, A1/B3 e B3/B5. No conjunto A1/A8, ao escolher o candidato “4” em A1, obrigatoriamente o número “2 será solução em A8, e vice-versa.

Links fracos:
Quando não se sabe a relação entre os números em uma UNIDADE.
Veja o Sudoku abaixo para o número “4”:
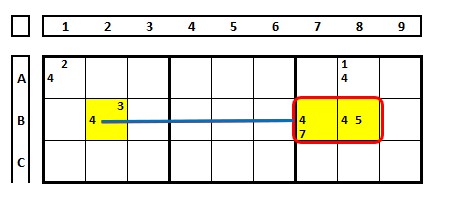
Não há certeza sobre a influência de um número “4” sobre o outro na linha B. Um ser “falso” não nos indica qual dos outros dois é verdadeiro.
A célula B2 (ou B5) não está na mesma UNIDADE que a célula A8. Cuidado, não é possível criar links entre eles.
No site será usado linha continua (azul) para links fortes e linha vermelha continua ou pontilhada para links fracos.
Links de grupo:
No exemplo abaixo, há uma forte inferência entre B2 e o conjunto B7/B8. Ou a solução para o número “4” está num ou noutro. Logo um link forte os une. Observe que entre B7 e B8 haverá um link fraco, pela presença do número “4” em B2 ou em A8. Mas, observe, há um link forte entre A8 e o conjunto B7/B8.
Complicado? Não se preocupe serão assuntos para mais tarde, em técnicas específicas.
Notação:
N = número de células
N+x = número de candidatos na célula (marcação de lápis)
Exemplo:
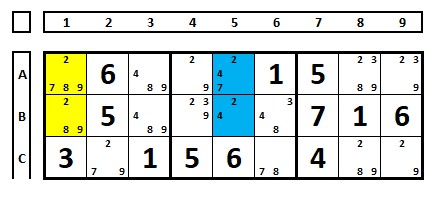
Notação das células marcadas em amarelo: N=2 (2 células) e N+x = N+2 (4 possibilidades: 2,7,8,9)
Notação das células marcadas em azul: N=2 (2 células) e N+x = N+1 (3 possibilidades: 2, 4, 7).
Em algumas técnicas esta notação será utilizada. Se a notação for “N+3”, significa que o número de células é “N” e o número de candidatos no conjunto de células é “N+3”.
Dica:
Para treinar o raciocínio, primeiro tente preencher as células (cruzamento de uma linha com uma coluna) sem colocar os “candidatos” possíveis nas células (marcação de lápis).
Ou seja, no início da solução, treine a memória e o raciocínio. Por exemplo, no Sudoku abaixo:
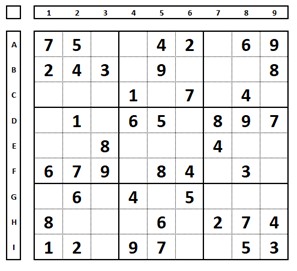
Não faça isto (colocar as marcações a lápis – ou candidatos – que poderiam ocupar as células para orientação):

O leitor perceberá rapidamente (com pouco treinamento) que o número “1” somente pode ocupar a célula A3, já que não pode, por conceito, ocupar as células C1, C2 e C3 (mesma linha, somente pode haver um número “1” nesta linha e este já ocupa a célula C4). Assim como o número “4” somente pode ocupar (no QM7) a célula I3. O número “5”, no QM2, a célula B4, e assim por diante.
Exercício: Tente resolver este Sudoku sem colocar numeração a lápis em cada célula.
Técnicas de resolução de Sudoku
Na próxima página iniciará a apresentação das técnicas. Na demonstração das técnicas, os mais experientes poderiam deduzir (identificar antes) a localização das soluções em algumas células, isto não é feito aqui para fins didáticos. As técnicas são ensinadas em ordem crescente de dificuldade (apesar de não apresentarem maiores dificuldades para seu entendimento). É recomendável acompanhar a ordem apresentada neste site que, de modo geral, corresponde a ordem apresentada por vários autores.
Foi, na medida do possível, identificado o nome da técnica também na língua inglesa, de forma a facilitar a busca de outras explicações e exemplos para a técnica em outros livros ou sites.

