Estes pares são também chamados de “pares trancados”, pois a solução de um leva a solução de todos.
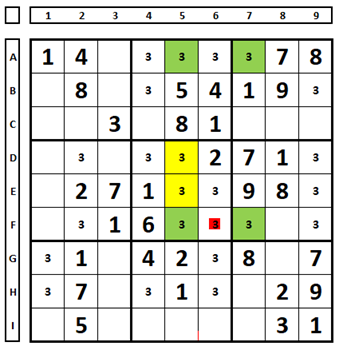
No Sudoku abaixo o número “6” pode estar presente como candidato em qualquer das células brancas e verdes. Não pode estar presente nas células marcadas em amarelo pela posição das pistas (A9, G6 e H3) Observar que para qualquer que seja a solução em B2 ou B4, a solução será inversa (em “x”, daí o nome da técnica) em D2 e D4. Se B2 for a solução D4 será solução e vice-versa. Com isto, os marcados em vermelho podem ser excluídos.


Finned and Filleted X-Wings:
Exemplo 1:
Exemplo 2:
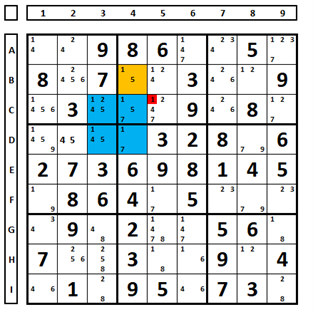
No exemplo abaixo há na coluna 3 dois números “1” e na coluna 4 dois números “1” formando um par alternado e mais um número “1” (em marrom). Um dos números “1” da coluna 3 é a solução. No entanto, na coluna 4 um dos dois números “1” em azul pertencerá a solução ou o número “1” em marrom pertencerá a solução. Com isto, pode-se excluir o número “1” da célula C5, pois para qualquer escolha feita na coluna 3 o número “1” da célula C5 será excluído.
As cores aqui usadas são para demonstração desta técnica e não são da técnica de coloração.
Exemplo 3:
O número “7” da célula E9 pode ser excluído, pois para qualquer um dos números “7” escolhidos na linha 1 ele será falso. Observe-se que o número “7” na célula E7 não pode ser excluído. (Se este número for solução na célula D4, será solução na célula E7).

Exemplo 4:
No Sudoku abaixo há um par para o número “6” na linha H (H5 e H9). Podemos formar um par na linha E (E5 e E9). As células marcadas em amarelo também pode ser solução para o Sudoku. Para qualquer escolha que se fizer na linha H, o número “6” na célula F5 poderá ser excluído.

Exemplo 5:
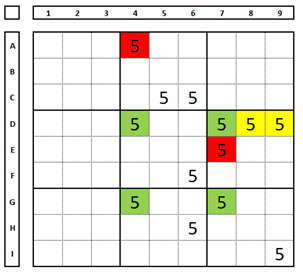
A escolha do número “5” na célula D4 deixaria a linha F sem solução, então este pode ser excluído. Logo, um dos números “5” da linha D do QM6 (D7, D8 ou D9) será solução. Com isto este número na célula E7 pode ser excluído.
Como o número “5” é solução na célula F6, este número pode ser excluído na célula H6, sendo este número solução na célula G4. As consequências são que este número na célula G7 pode ser excluído, é solução na célula I9 e solução na célula D7.
Bom treinamento, pegue este Sudoku e considere como corretas cada uma (uma a uma) das quatro possibilidades na linha D.
Exemplo 6:
O número “1” pode ocupar somente duas células na linha A. Observe que, para qualquer escolha que for feita como correta na linha A, o número “1” na célula E5, pode ser excluído. O Sudoku abaixo é para demonstração, pois o número “1” ocupa somente uma célula na linha F, logo também excluiria o número “1” da célula E5. É comum várias técnicas chegarem a mesma conclusão e não poderia ser diferente, já que o Sudoku deve ter somente uma solução.

Exemplo 7:
Exercite sua mente. O número “7” em E5 é solução nesta célula.


