Muitos autores dizem que é a técnica mais próxima de “uma solução de tudo” em um Sudoku.
Uma Cadeia de Inferência Alternada , mais conhecida por sua sigla AIC , é uma cadeia de premissas, ligada por alternância de inferências fortes e fracas .
Um aviso, é muito fácil se enganar na construção desta técnica. Vá com cuidado. E não é a solução de tudo, apenas mais uma técnica.
Pode-se dizer que AICs englobam uma série de técnicas vistas anteriormente, que são explicadas inicialmente por que apresentam visualização simples de serem percebidas, como X-Wing, Correntes XY, XYZ-Wings e muitas outras.
Todas as correntes começam com a relação entre números (candidatos) ou grupos de números, normalmente iniciando, mas não necessariamente, com links fortes. E os links vão se sucedendo entre fortes/fracos até o momento que indicam uma solução ou eliminação no Sudoku.
A diferença básica com os X-Cycles é que estes ligam o mesmo número através do Sudoku, enquanto as AICs ligam, por links forte/fracos, diferentes números.
Esta técnica envolve usar técnicas já vistas para a construção das cadeias X-Cycles, os Nice Loops.
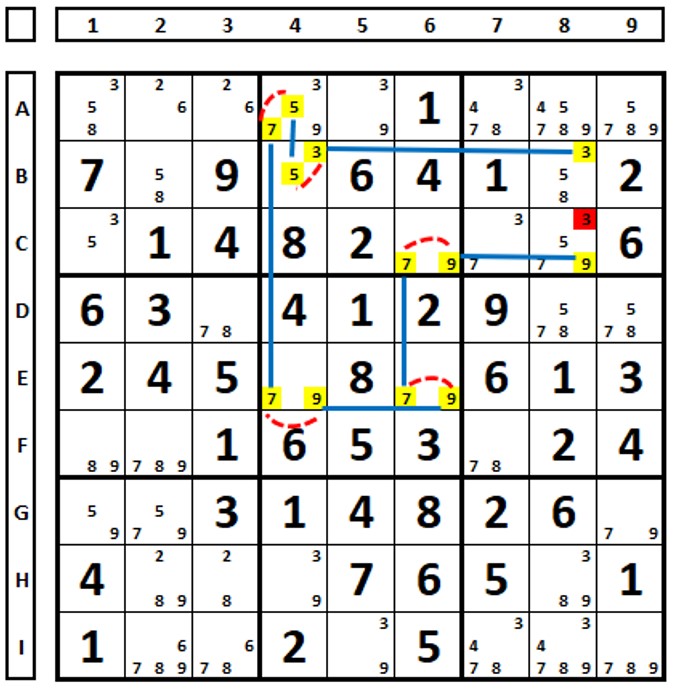
Começando com um exemplo simples. No sudoku abaixo, os números “5” e ”7” são unidos por links fortes (são os únicos em sua coluna) e por links fracos, pois há outros candidatos nas duas células onde se encontram. Pelas regras dos Nice Loops, os números marcados em vermelho podem ser excluídos, já que é um Loop contínuo. O exemplo é simples pois seria resolvido de outra forma, já que os números “5” e “7” só se encontram nestas duas células na coluna 8.
Tipos de links em Nice Loops:
Deve haver um link unindo duas células em um Nice Loop. Um link forte pode ser usado para inferência forte ou fraca, mas um link fraco só pode ser usado para inferência fraca. Tipos de links:
Regras de propagação:
A propagação dos links entre os candidatos que se encontram nas células tem as seguintes regras:
Verifique se o elo da célula anterior no Loop segue as regras, senão não vá adiante.
Loops agradáveis contínuos e descontínuos
Para determinar se um Nice Loop é contínuo ou descontínuo deve-se examinar o primeiro e o último nó, representando a mesma célula. Quando os dois links para aquela célula obedecem às regras de propagação, o loop é contínuo, caso contrário, é descontínuo.
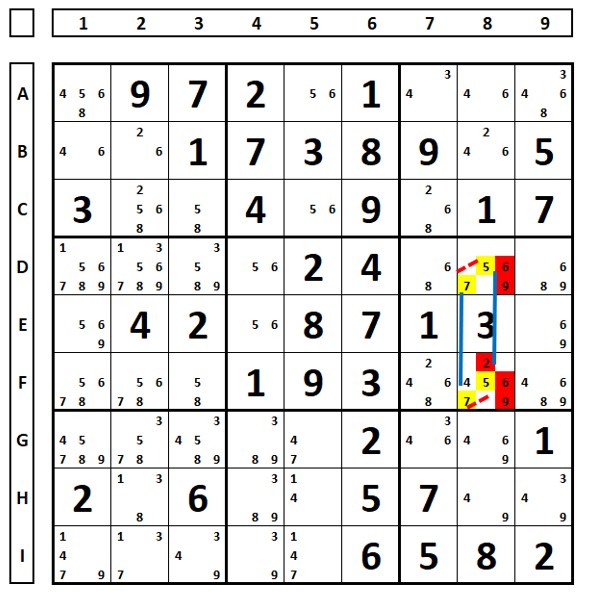
Exemplo de sudoku descontinuo. Neste sudoku não há a sequência links fortes e fracos, há descontinuidade na célula A7 aonde chegam dois links fortes. O número “3” da célula A7 é solução nesta célula pelo encontro de dois links fortes. O número “4” da célula G7, bem como os números “6” das células B8, D8 e F8 não podem ser excluídos pois não é um loop contínuo (regra dos Nice Loops).
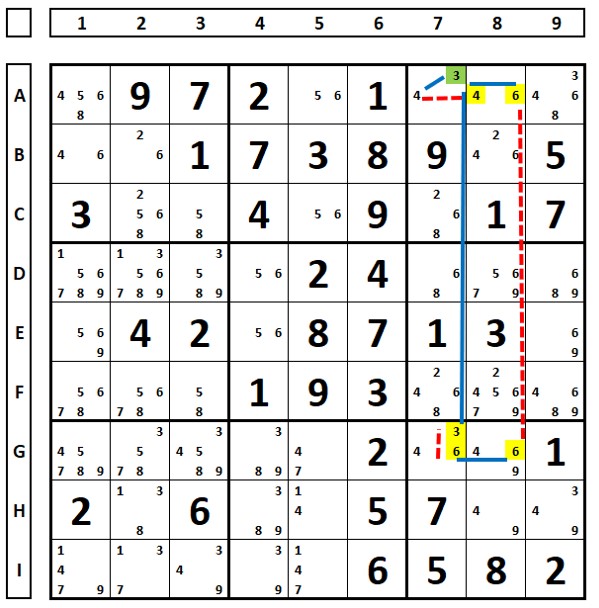
Na célula A7 há um vínculo forte entre os dois candidatos (3, 4) pois são os únicos dois possíveis nesta célula (um será solução e o outro não). O número “4” da celula A7 tem um vínculo fraco com este mesmo número na célula A8 (pois há este mesmo número nas células A1, A9 e B8). O número “6” (A8) tem vínculo fraco com este mesmo número na célula G8 e forte da célula G8 para a célula G7. O número “6” (G7) tem um vínculo fraco com o número “3” na mesma célua (pela presença do candidato “4”). E o número “3” tem vinculo forte com este mesmo número na célula A7.
Loops agradáveis contínuos
São aqueles que a regra de propagação não é quebrada entre o penúltimo e o último (primeiro) elo do Loop (sempre fechado).
Todas as células do Loop são olhadas para a descoberta da continuidade e, com isto, manter ou eliminar um candidato no Loop ou em outro ponto de uma UNIDADE.
Regras:
No sudoku abaixo há um ciclo contínuo, as linhas verdes são links fortes transformados em links fracos. Os números em vermelho podem ser excluídos.

No Sudoku abaixo, os links fortes foram transformados em links fracos (em verde). Há continuidade em toda a cadeia. O número “7” em I6 pode ser excluído.
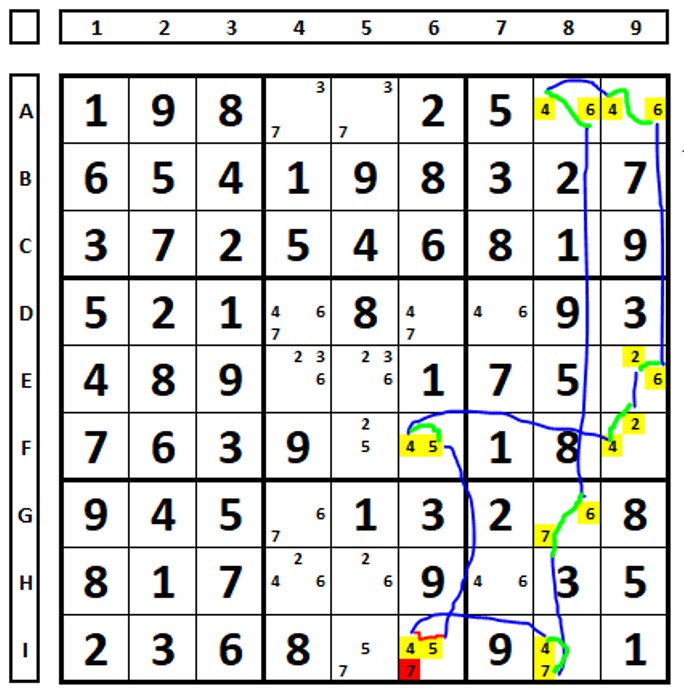
Observe o loop contínuo abaixo (links verdes – fortes transformados em fracos).
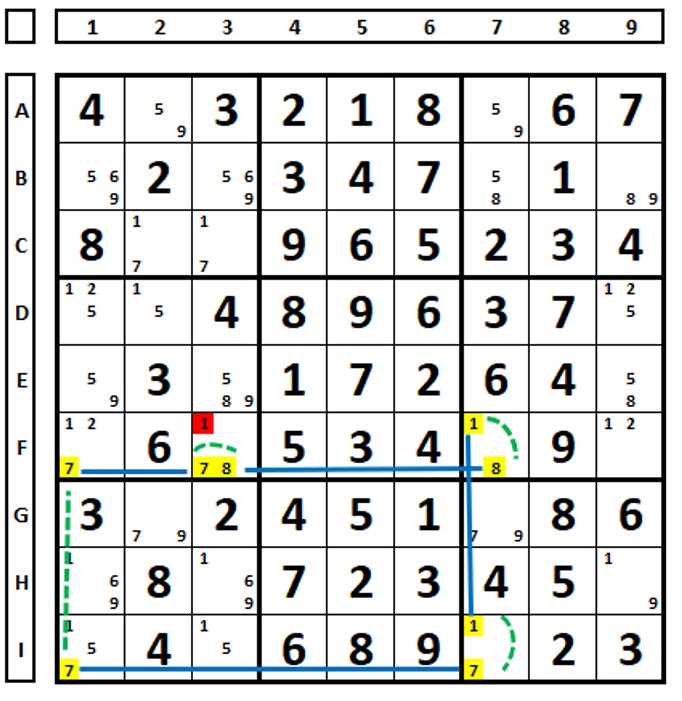
Loops agradáveis descontínuos:
Quando o Loop retorna à primeira célula em contradição ao candidato escolhido para início da cadeia.
O Nice Loop descontinuo é o mais comum num Sudoku. A célula inicial e final (a mesma célula) é chamada de descontinuidade.
O que pode acontecer na primeira célula no fim do Loop:
Descontinuidade na célula inicial com dois elos fracos:
Se a célula inicial tiver dois elos fracos para o mesmo candidato, esse candidato pode ser eliminado da célula. Os links dentro das células não foram marcados para não poluir, mas observe que é uma sequência links fortes/fracos com descontinuidade na célula A1.
Iniciando o Sudoku em A1, com o número “4”.
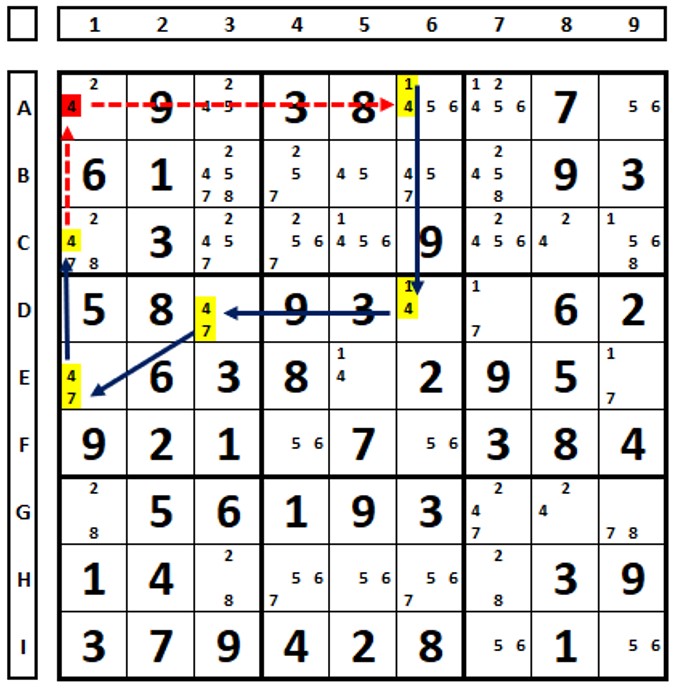
O exemplo abaixo mostra o poder da técnica:
No QM3, liga-se o número “6” da célula A8, ao número “5” da célula A9. Por quê? Se um for solução em uma célula o será em outra, link forte. As marcações em verde são links fortes transformados em fracos. Os vermelhos links fracos.
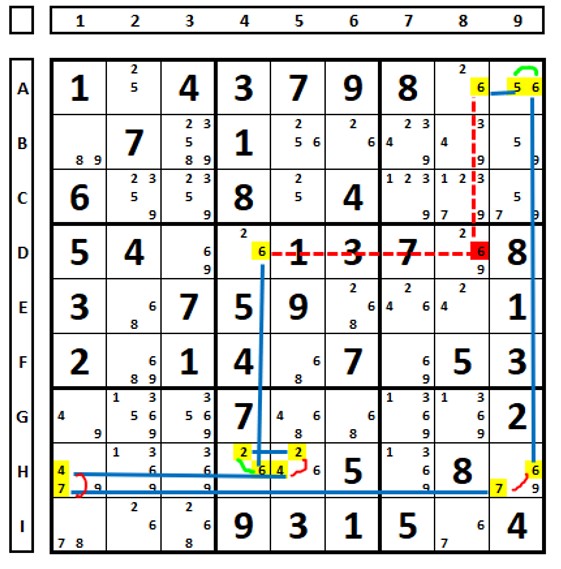
Descontinuidade com dois elos fortes chegando na célula inicial:
Se a célula inicial (E8) tiver dois vínculos fortes com o mesmo candidato, pode ser resolvido com o candidato da célula.
Número “9” solução em E8.
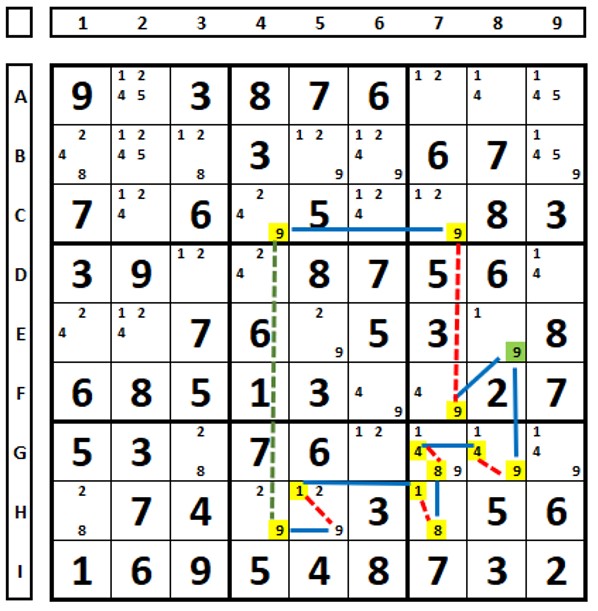
Descontinuidade com um elo fraco e um forte na célula inicial:
Se a célula inicial contiver um vínculo fraco e um vínculo forte com diferentes candidatos, o candidato do vínculo fraco pode ser eliminado da célula.
No sudoku abaixo, o número “9” pode ser excluído na célula B7. Não se sabe se o número “5” ou o número “7” será solução nesta célula.
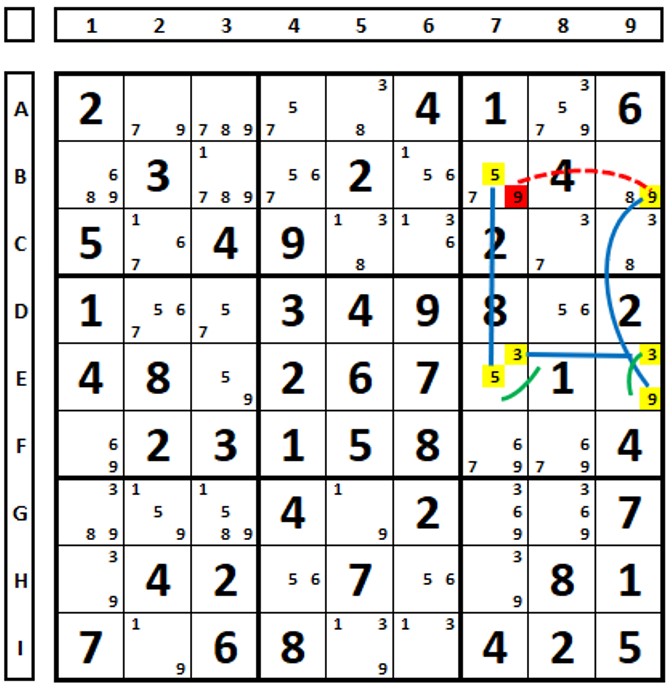
Loops agradáveis complexos
Aqui usa-se um grupo de células no Loop, como já foi visto anteriormente nos X-Cycles.
No sudoku contínuo abaixo, links verdes (fortes para fracos).
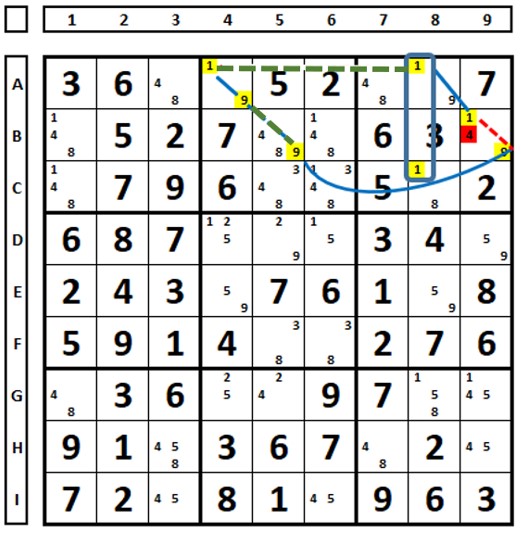
No sudoku abaixo, na célula C5, o link forte foi transformado em link fraco (em verde). O número “7”, na célula H1 é solução, pois é união de dois links fortes.
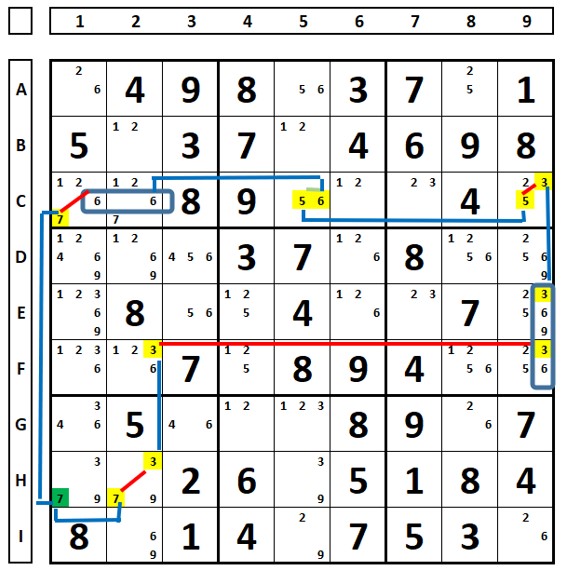
Um AIC Tipo 1 começa e termina em um link forte para o mesmo digito em duas células. Como um dos dígitos será solução do sudoku, o mesmo digito que veja estas duas células ao mesmo tempo pode ser excluído.
Examinando o sudoku abaixo para o número “8”. O número “8” na célula D4 pode ser excluído pois enxerga as células D2 e B4, onde os números “8” estão com links fortes chegando neles.
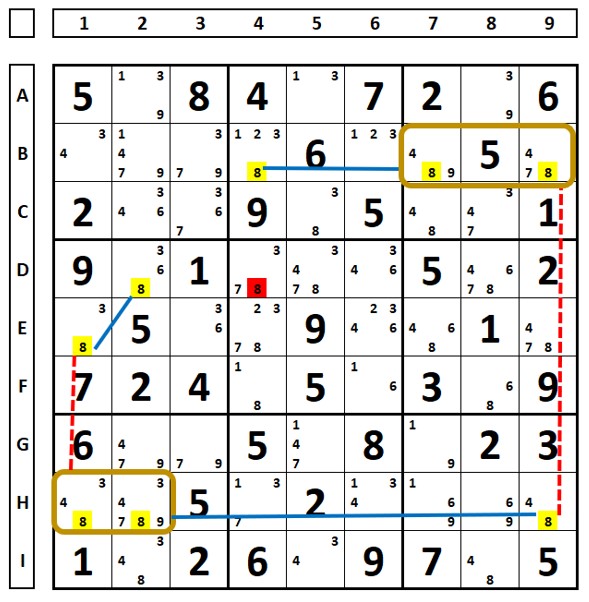
No sudoku abaixo, todos os links fortes foram transformados em fracos, o que permitiu a exclusão do número “7” na célula H3.
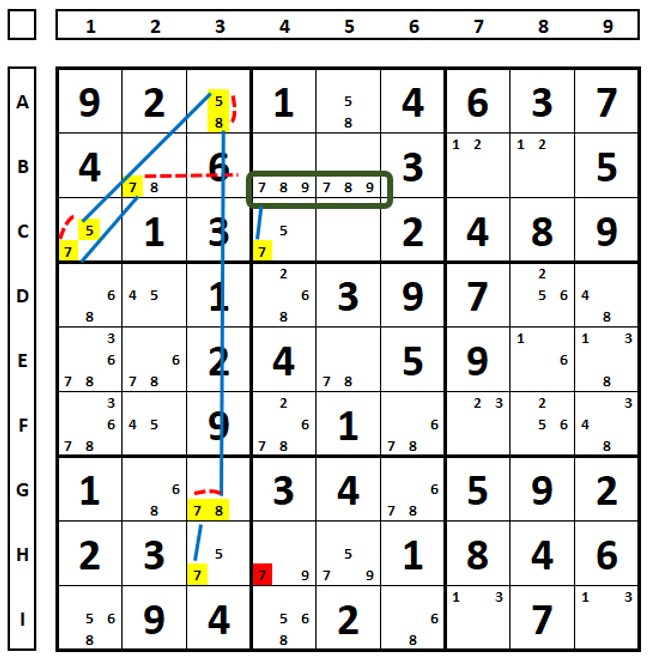
Neste sudoku, todos os links fortes também forma transformados em fracos, o que permitiu a exclusão do número “8” da célula G4:
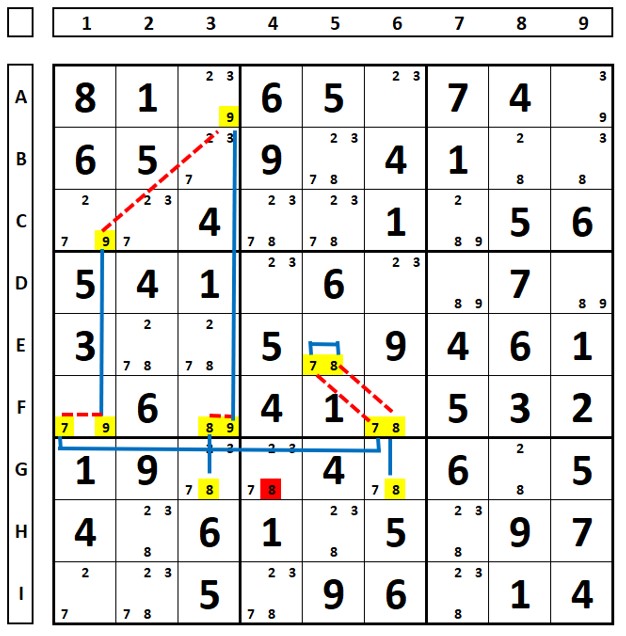
Um AIC Tipo 2 começa e termina em um link forte para dois dígitos diferentes em duas células, que se veem. Isso demonstra que o dígito final não pode estar na célula inicial e o dígito inicial não pode estar na célula final.