Many authors say that the technique closest to an “all-in-one solution” in Sudoku is the Alternating Inference Chain (AIC), which is a chain of premises linked by alternating strong and weak inferences.
A word of warning, it is very easy to make mistakes in constructing this technique. Proceed with caution.
It can be said that AICs encompass a series of techniques previously seen, initially explained for their simple visualization, such as X-Wing, XY Chains, XYZ-Wings, and many others.
All chains start with the relationship between numbers (candidates) or groups of numbers, typically starting but not necessarily with strong links.
And the links continue alternating between strong/weak until they indicate a solution or elimination in Sudoku.
The basic difference with X-Cycles is that they link the same number throughout the Sudoku, while AICs link different numbers through strong/weak links, much like the 3D-Medusa technique. It’s interesting to note that this technique can involve using previously seen techniques to construct the chains.
Here a new type of link (strong) is shown, in addition to the strong/weak links already discussed in the site.
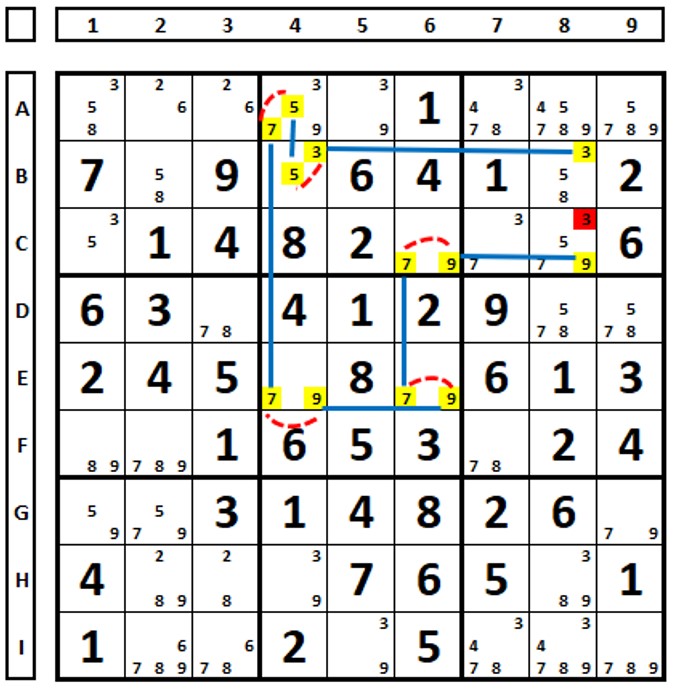
In the Sudoku below, part of a chain is shown. Why does the number “6” (A8) connect through a strong link (blue) with the number “5” (A9)? Both, by choosing one or the other, will solve the cells, which allows the creation of a strong link (in green), which is then transformed into a weak link to continue the chain.
Types of links in Nice Loops:
There must be a link joining two cells in a Nice Loop. A strong link can be used for either strong or weak inference, but a weak link can only be used for weak inference. Types of links:
Propagation rules:
The propagation of links between candidates that are in cells has the following rules:
Check if the link from the previous cell in the Loop follows the rules; if not, do not proceed.
Continuous and discontinuous Nice Loops
To determine whether a Nice Loop is continuous or discontinuous, you must examine the first and last node, representing the same cell. When the two links to that cell obey the propagation rules, the loop is continuous; otherwise, it is discontinuous.
For example, in this Sudoku, there is a discontinuous sequence of links. There is a discontinuity in cell A7 where two strong links arrive. The number “3” in cell A7 is a solution in this cell due to the intersection of two strong links. The number “4” in cell G7, as well as the numbers “6” in cells B8, D8, and F8, cannot be excluded because it is not a continuous loop (Nice Loops rule).
In cell A7 there is a strong link between the two candidates (3, 4) as they are the only two possible in this cell (one will be the solution and the other will not). The number “4” in cell A7 has a weak link with the same number in cell A8 (as there is the same number in cells A1, A9, and B8). The number “6” in cell A8 has a weak link with the same number in cell G8 and a strong link from cell G8 to cell G7. The number “6” in cell G7 has a weak link with the number “3” in the same cell (due to the presence of the candidate “4”). And the number “3” has a strong link with the same number in cell A7.
Continuous nice loops
Are those where the propagation rule is not broken between the penultimate and last (first) link of the loop (always closed).
All cells in the loop are checked for continuity and, with this, to maintain or eliminate a candidate in the loop or at another point in a unit.
Rules:
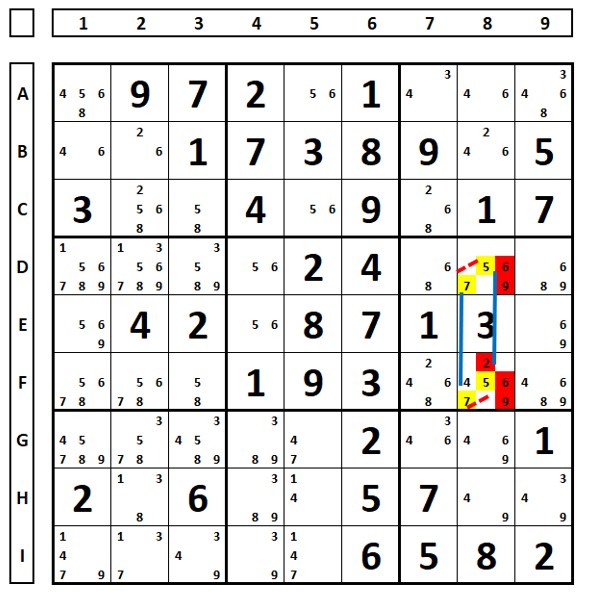
In the sudoku below, there is a continuous loop, the green lines are strong links transformed into weak links. The numbers in red can be eliminated.

In the Sudoku below, the strong links have been transformed into weak links (in green). There is continuity throughout the chain. The number “7” in I6 can be eliminated.
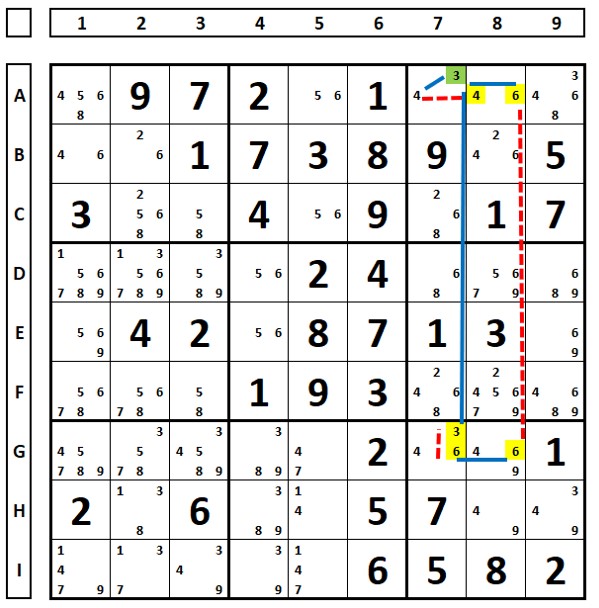
Observe the continuous loop below (green links – strong transformed into weak).
Discontinuous nice loops:
When the loop returns to the first cell in contradiction to the candidate chosen to start the chain.
The discontinuous nice loop is the most common in Sudoku. The initial and final cell (the same cell) is called a discontinuity.
What can happen in the first cell at the end of the loop:
Discontinuity in the initial cell with two weak links:
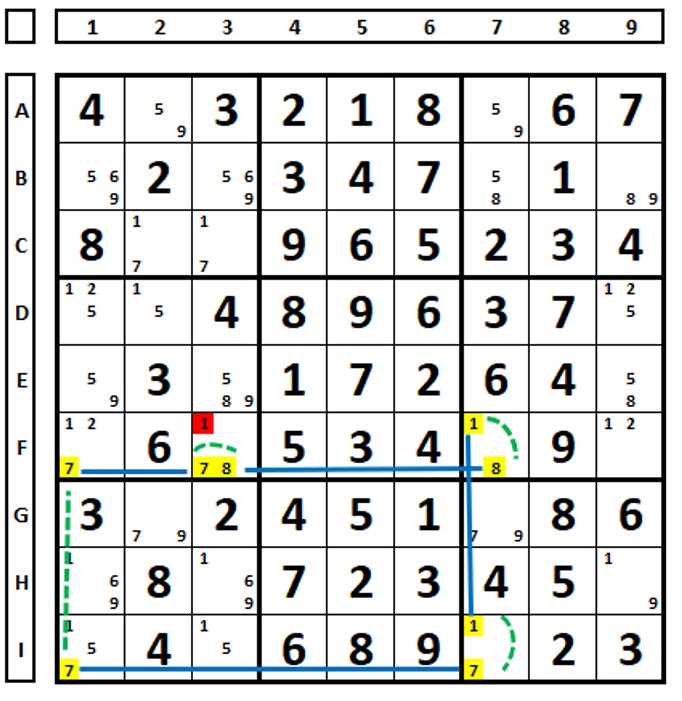
If the initial cell has two weak links to the same candidate, that candidate can be eliminated from the cell. The links within the cells were not marked so as not to clutter, but note that it is a sequence of strong/weak links with a discontinuity in cell A1.
Starting the Sudoku in A1, with the number “4”:
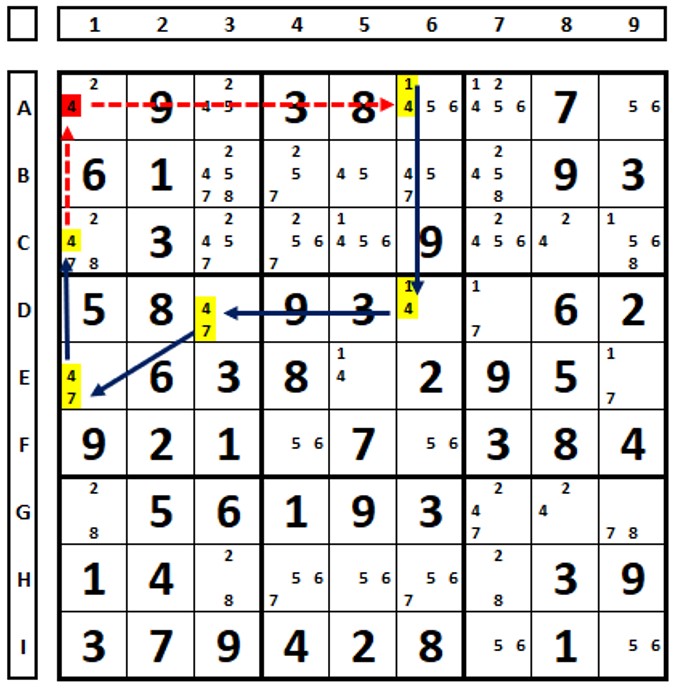
The example below shows the power of the technique:
In box 3, the number “6” in cell A8 is connected to the number “5” in cell A9. Why? If one is a solution in a cell, it will be in another, strong link. The green markings are strong links transformed into weak links. The red markings are weak links.
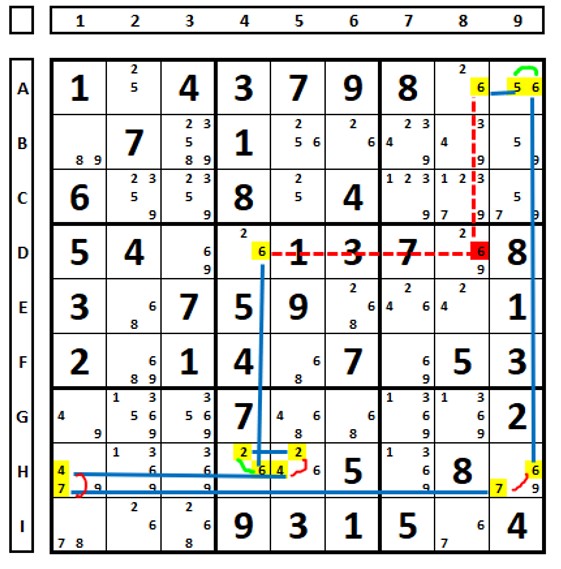
Discontinuity with two strong links arriving at the initial cell:
If the initial cell (E8) has two strong links to the same candidate, it can be solved with the candidate in the cell.
Number “9” is the solution in E8.
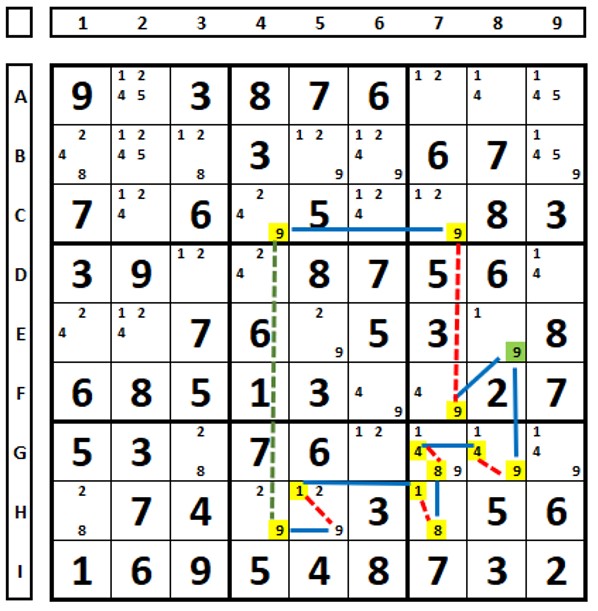
Discontinuity with one weak link and one strong link in the initial cell:
If the initial cell contains one weak link and one strong link with different candidates, the candidate in the weak link can be eliminated from the cell.
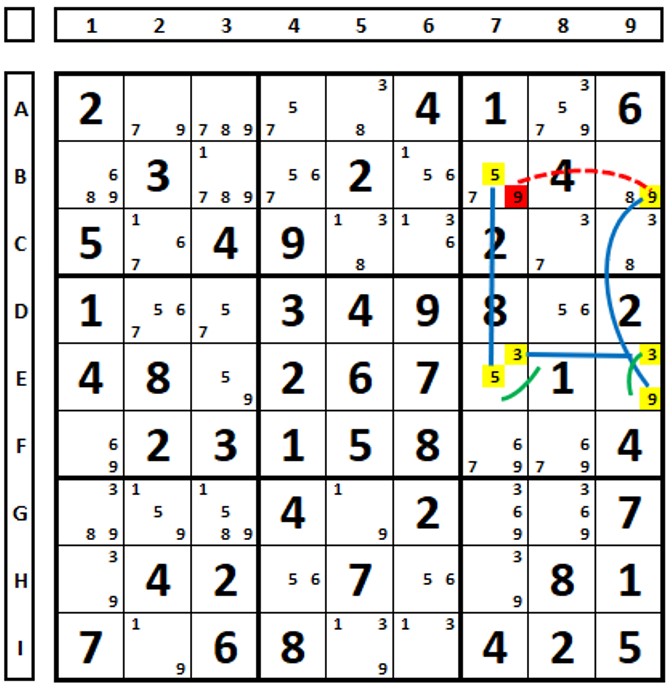
In the Sudoku below, the number “9” can be eliminated in cell B7. It is not known whether the number “5” or the number “7” will be the solution in this cell.
Complex Nice Loops
Here a group of cells is used in the loop, as previously seen in X-Cycles.
In the continuous Sudoku below, green links (strong to weak).
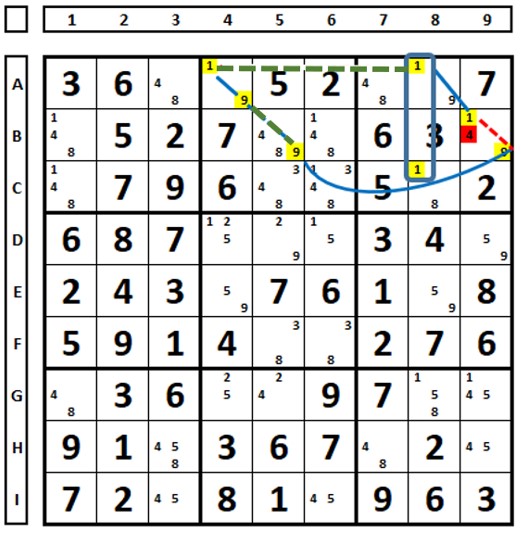
In the Sudoku below, in cell C5, the strong link was transformed into a weak link (in green). The number “7” in cell H1 is the solution, as it is the union of two strong links.
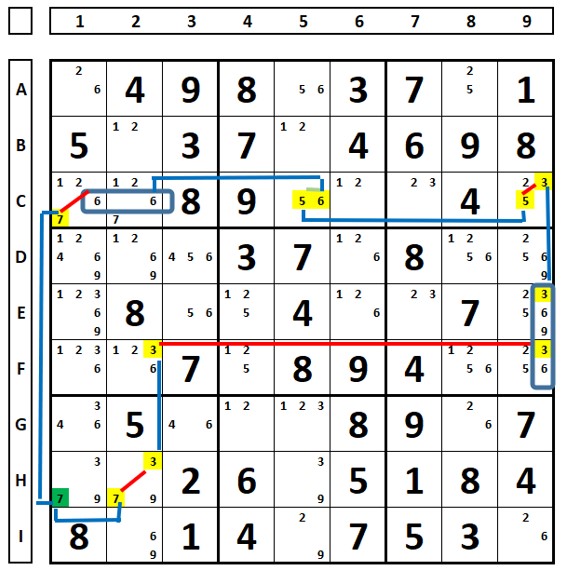
AICs – Open Chains.
Type 1 alternate inference chain
A Type 1 AIC begins and ends with a strong link for the same digit in two cells. Since one of the digits will be a solution to the sudoku, the digit that sees these two cells at the same time can be excluded.
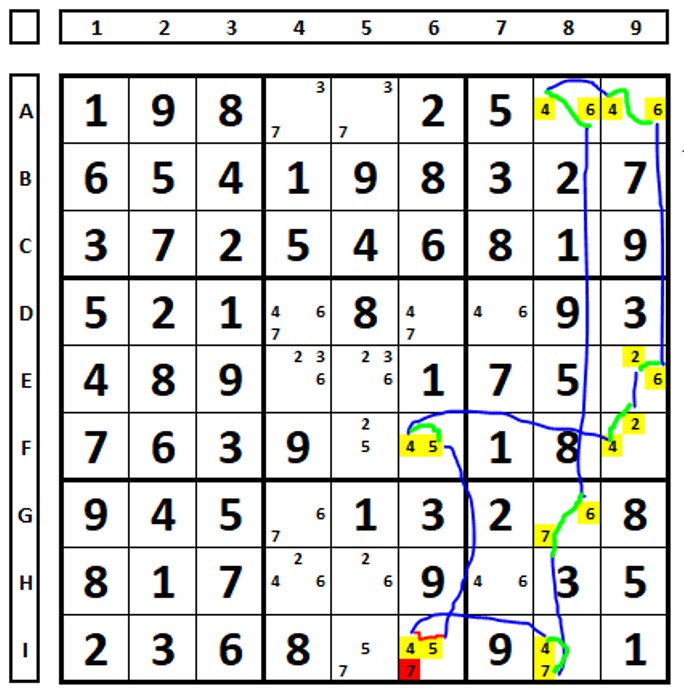
Examining the sudoku below for the number “8”. The number “8” in cell D4 can be excluded as it sees cells D2 and B4, where the numbers “8” have strong links reaching them.
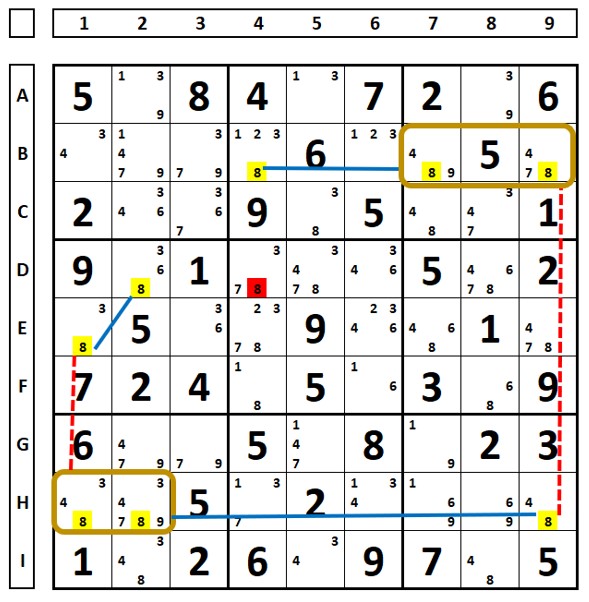
In the Sudoku below, all strong links were transformed into weak links, which allowed for the exclusion of the number “7” in cell H3.
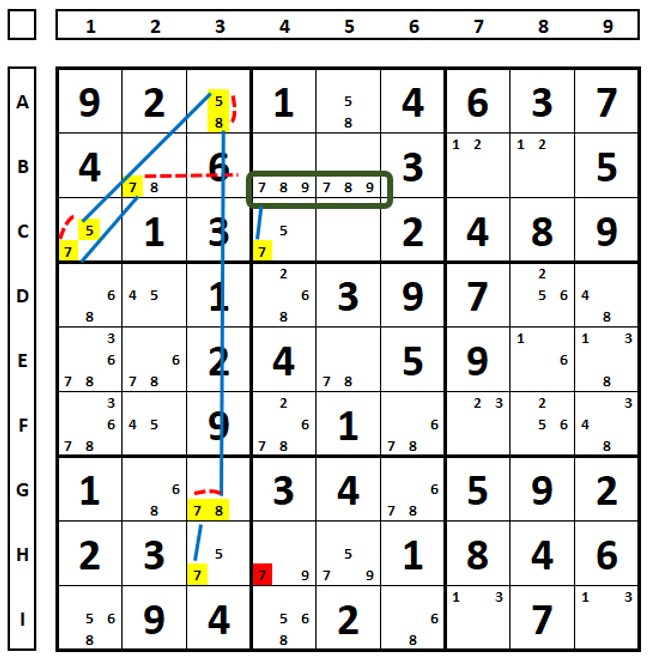
In this Sudoku, all strong links were also transformed into weak links, which allowed for the exclusion of the number “8” from cell G4:
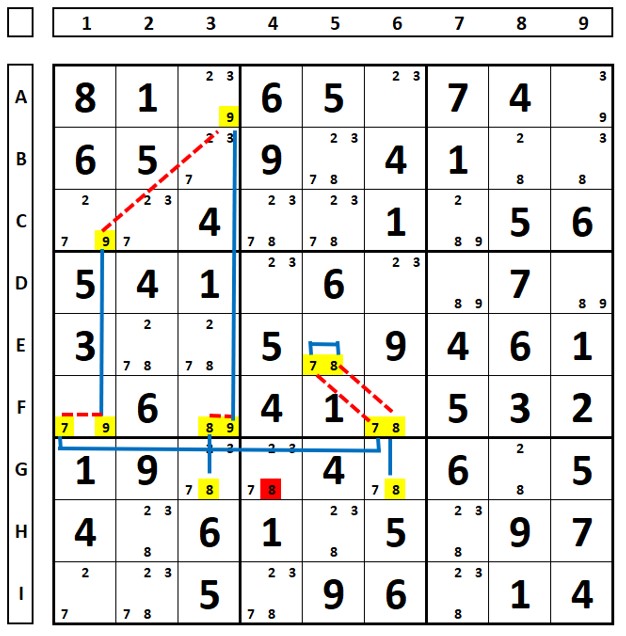
Alternative Inference Chain type 2
An AIC Type 2 starts and ends in a strong link for two different digits in two cells that see each other. This demonstrates that the final digit cannot be in the initial cell and the initial digit cannot be in the final cell.