Como já foi visto, um conjunto bloqueado é o que tem N células e N candidatos. Por exemplo, um Naked Pair. Revendo um exemplo do livro. No QM abaixo, as células em amarelo são um Naked Pair ou conjunto bloqueado, N (=2) células com N+0 (=2) candidatos possíveis. Ou seja, dois candidatos em duas células.
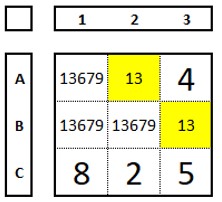
Os conjuntos quase bloqueados ou ALS são um conjunto de células com exatamente um candidato extra (é “quase bloqueado”, longe de ser bloqueado). Notação N+1.
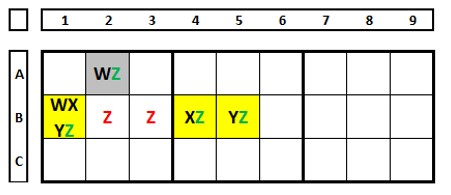
Um XY-Wing é uma maneira interessante de demonstrar ALSs, conforme exemplo abaixo. No primeiro ALS em amarelo, duas células (N) em contém três números (4,5,7) (N+1). No segundo ALS em verde, uma célula (N) e dois números (7,5) (N+1). O número “5” do ALS verde, “enxerga” todos os números “5” do ALS amarelo. O número “7”, em vermelho (célula I2), enxerga ambos os números “7” nos dois ALSs, por isto pode ser excluído. É fácil, neste exemplo, demonstrar isto, só de olhar. Caso o número “7” fosse solução em I2, no QM9 restariam dois números “4” (em H7 e I9) o que contraria a regra (dois números iguais no mesmo QM).

Olhando um exemplo XYZ-Wing já visto anteriormente. O exemplo foi deixado – o colorido – na forma de XYZ-Wing. Onde estão os ALSs? No conjunto D3/F2 há um N+1 (duas células e três possibilidades: (1,4,6). O outro ALS é a célula A2 onde há um N+1 (uma célula e duas possibilidades). O número “1” em A2, enxerga todos os números “1” no segundo conjunto (D3/F2). O número “6” em E2 pode ser excluído, pois enxerga todos os números “6” nos dois conjuntos.
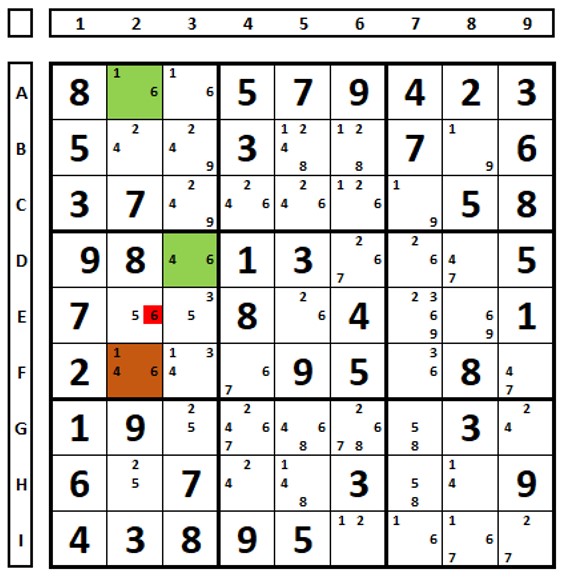
Dados os exemplos, a regra é um número (x) é comum aos dois ALSs e este número enxerga todos os mesmos números (x) no outro conjunto. Ambos os ALSs têm um número (y) comum aos dois, mas que não se enxergam. Os números (y) nas células estranhas aos ALSs, mas que enxergam os números (y) nos dois ALSs podem ser excluídos.
O “x” também é chamado de Candidato Comum Restrito (CCR ou em inglês RCC). É solução num ALS ou no outro.
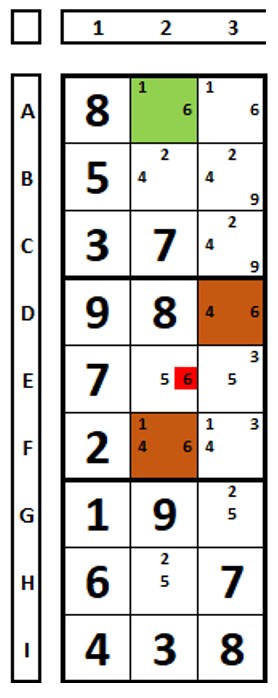
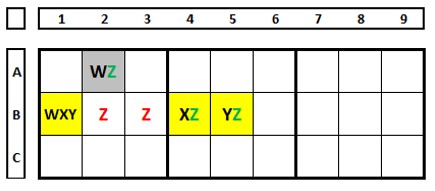
No mesmo exemplo acima, agora na forma de ALSs (abaixo). O número “1” (nosso “x”) no ALS verde enxerga todos os números “1” no ALS marrom. O número “1” é comum aos dois ALS. O número “6” (nosso “y”) é comum aos dois ALSs, mas o número “6” no ALS verde não enxerga todos os números “6” no ALS marrom (em D3). O número “6” na célula E2 enxerga todos os números “6” nos dois conjuntos e pode ser excluído desta célula.
Examine com cuidado a utilidade do Candidato Comum Restrito. No Sudoku abaixo, ou o número “1” é solução no ALS verde ou no ALS marrom. Se for no verde, exclui o número “1” em F2 e teremos um Par Bloqueado (Naked Pair) em D3/F2 (4,6), com isto o número “6“seria excluído em E2. Caso o número “1” fosse solução no ALS marrom, o número “1” seria excluído no ALS verde, restando o número “6” em A2, o que também excluiria o número “6” em E2.
Como foi observado anteriormente, WXYZ-Wing são ALS.
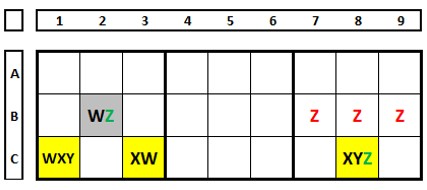
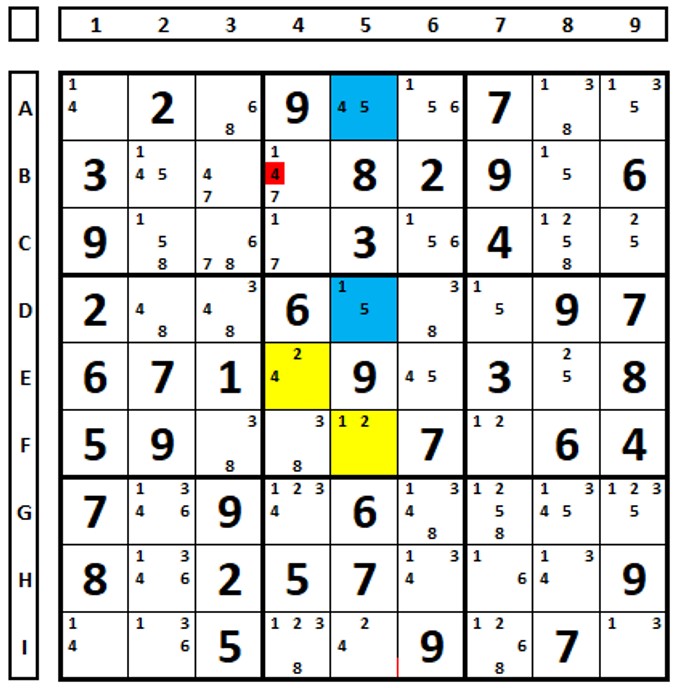
No Sudoku abaixo há dois ALSs, um em azul e outro em amarelo, ambos N+1. Os números “1”, em ambos os conjuntos se enxergam, o número “4”, comum a ambos, mas não restrito, permite excluir o número “4” em B4. E com isto solucionar rapidamente este sudoku. Faça a prova dos nove, escolha o número “4” como solução em B4 e veja o que acontece na coluna 5 do QM5.
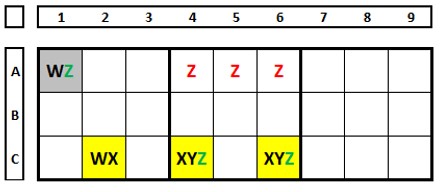
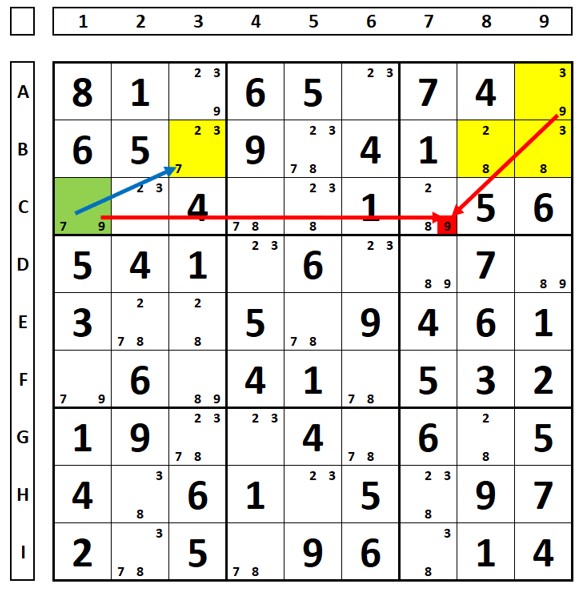
No sudoku abaixo há o ALS marcado em amarelo e o em verde. O número “7” é RCC em ambos. O número “9” da célula C7 enxerga todos os números “9” dos dois ALSs e pode ser excluído.
Os ALS ou com vínculo único são os modelos que foram demonstrados acima.
ALS podem se sobrepor em todas as técnicas de ALS. Há apenas uma restrição: a área de sobreposição entre dois ALS não deve conter um CCR (RCC).
No sudoku abaixo dois ALSs em verde a amarelo, com os números “2” e “5” como Comuns Restritos.
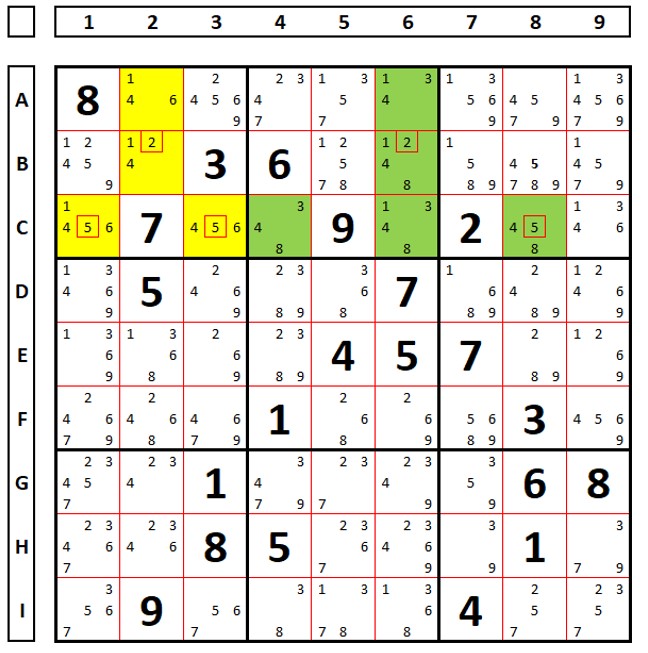
O que acontece quando se escolhe um Comum Restrito como solução? A escohermos o número “2” na célula B6 o conjunto amarelo fica bloqueado com quatro células e quatro números (1,4,5,6). Ao se escoher o número “5” na célula C8 há também o bloqueio no conjunto amarelo. Ao se inverter a escolha usando o conjunto amarelo, ocorre o mesmo bloqueio no conjunto verde.
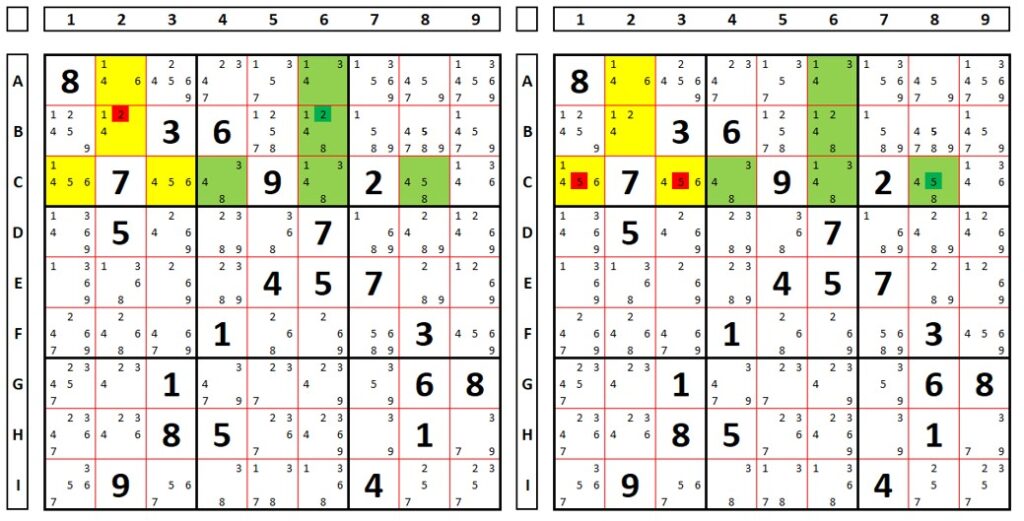
Qual a consequência? Todos os números que vêem todos os RCCs dos dois conjuntos podem ser excluídos, bem como os que vêm os não Comuns Restritos na Unidade.
O número “2” na célula B1 pode ser escluído pois enxerga os dois números “2” (que são RCCs) nos dois ALSs.
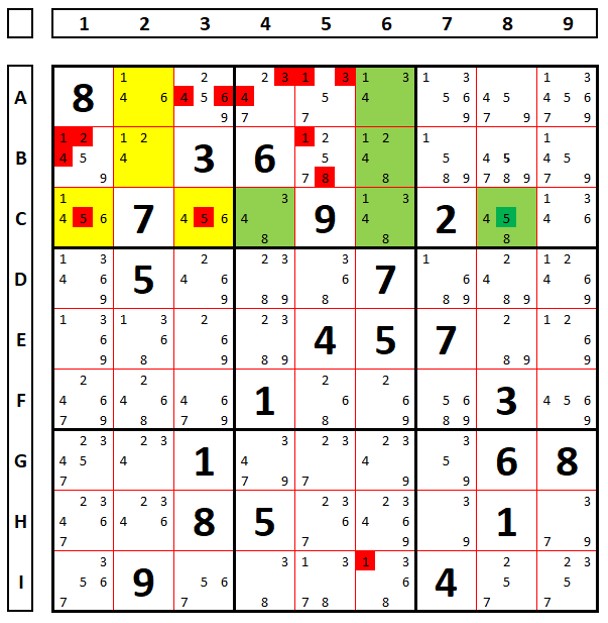
No Sudoku abaixo há dois comuns restritos (os números “7” e “9”). Um será solução em um ou em outro, com isto pode-se excluir o número “9” na célula G2, que enxerga os dois números “9” dos dois ALSs.
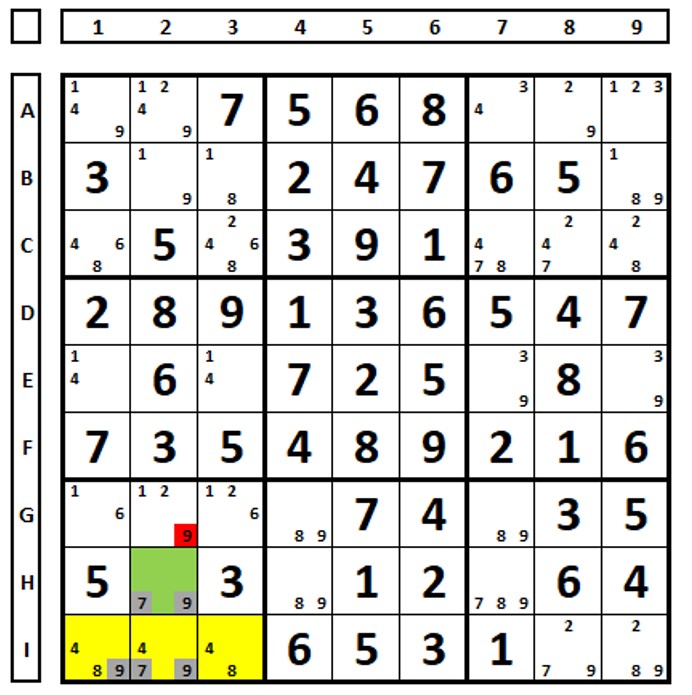
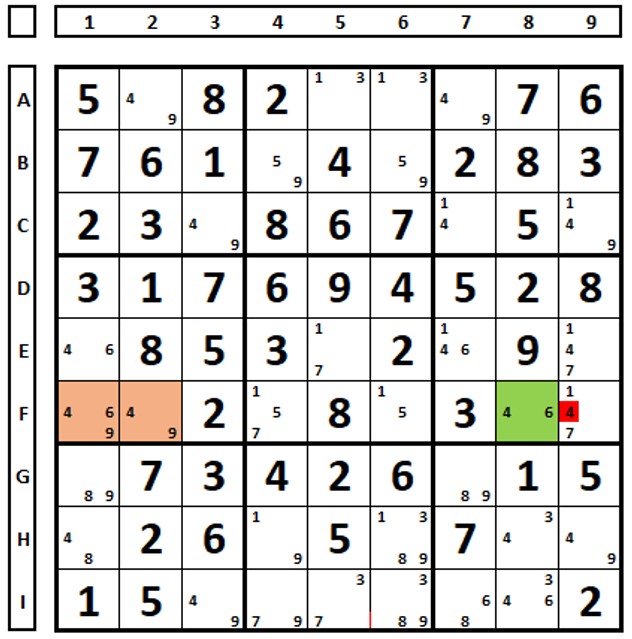
No sudoku abaixo há os dois ALSs marcados em amarelo e verde, com os números “3” e “9” marcados como RCC. O número “7” da célula C3 enxerga todos os números “7” do ALS verde e pode ser excluído.
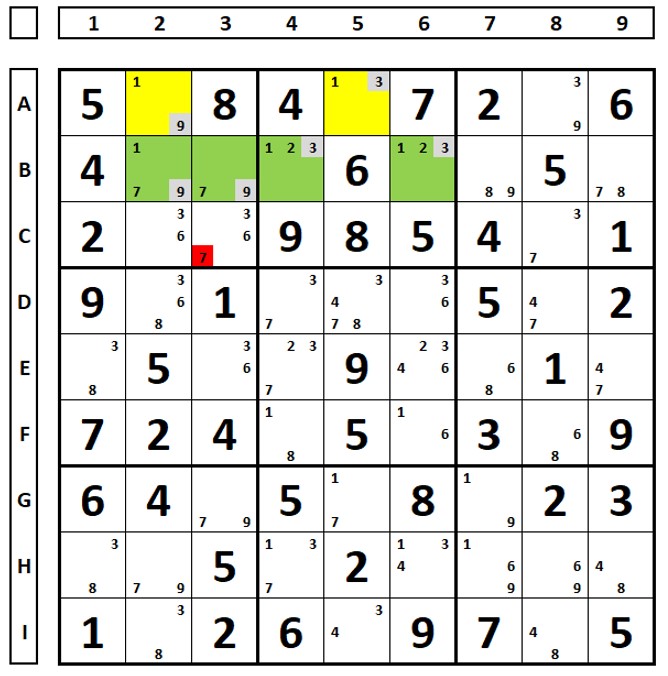
No sudoku abaixo são mostradas todas as regras de eliminação possíveis com o ALS de duplo vínculo. Os RCC comuns aos dois são os números “3” e “8”, com isto os números “3” nas células E4 e E6 podem ser excluídos pois enxergam os RCC dos dois ALSs. O número “3” da célula D2 pode ser excluído pois enxerga todos os números “3” dos dois ALSs. O número “6” na célula E6 pode ser excluído pois enxerga todos do ALSs verde.
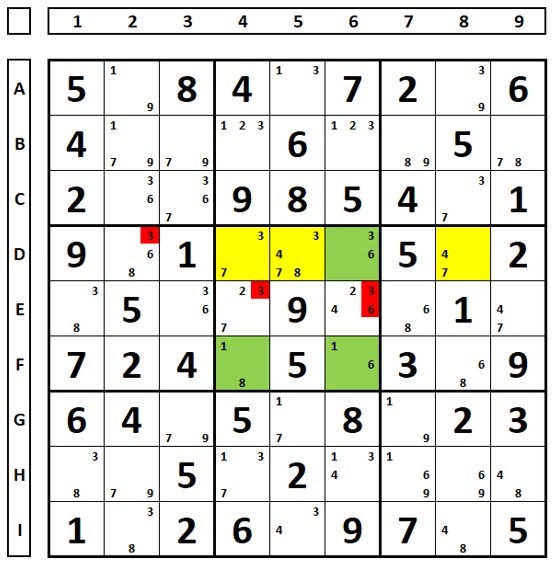
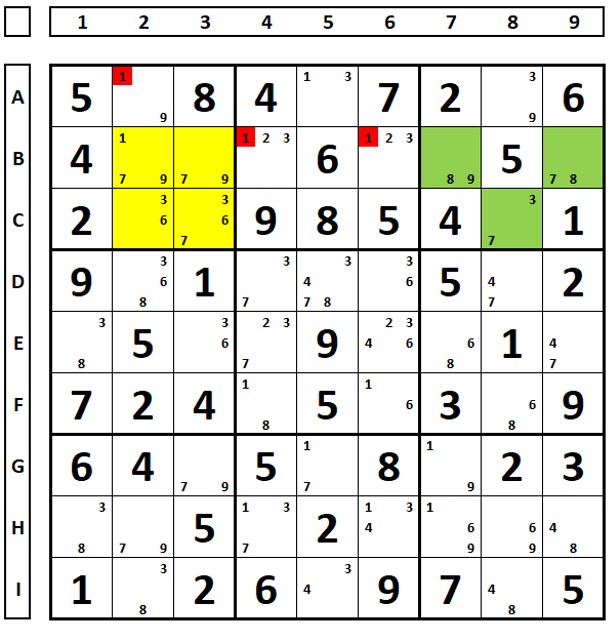
No mesmo sudoku, os RCC dos dois ALSs são os números “3” e “9”. Os números “1” marcados em vermelho podem ser excluídos pois enxergam “todos” os números “1” do ALS amarelo.
ALS – XY – Wing
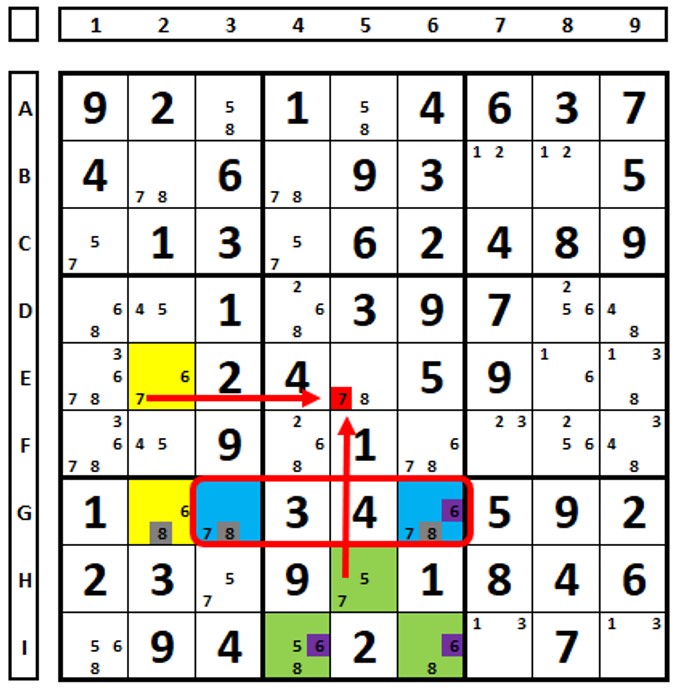
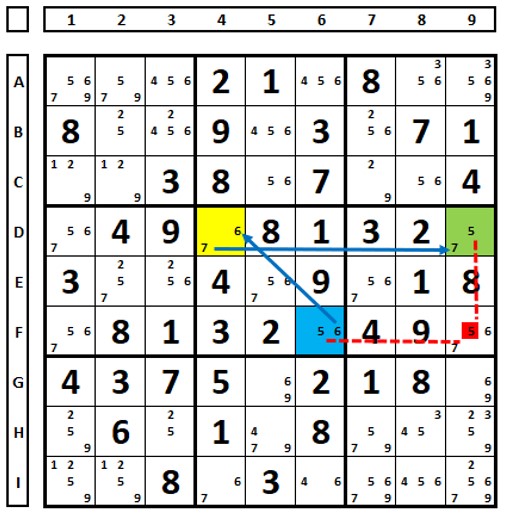
No Sudoku abaixo, na técnica XY-WING, qualquer escolha na célula em amarelo, leva ao número “5” na célula azul ou na verde, excluindo o número “5” na célula F9.
Na técnica ALS-XY-Wing há três ALS (verde, azul e amarelo). O número “6” em F6 é comum restrito com o mesmo número em D4. O número “7” em D4 é comum restrito com o mesmo número em D9. O número “5” em F9 pode ser excluído, pois enxerga ambos os números “5” na ponta da cadeia (células azul e verde).