Aqui vamos usar o conceito de “enxergar”. Esta estratégia foi desenvolvida inicialmente com a regra:
Quaisquer duas células alinhadas em uma linha ou coluna dentro da mesma caixa não podem duplicar o conteúdo de qualquer célula de duas candidatas que as duas visualizarem.
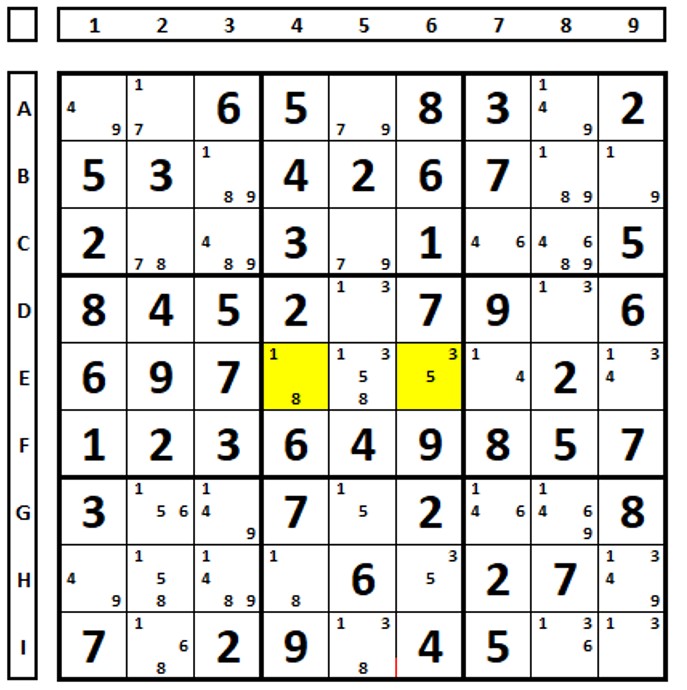
Exemplo neste sudoku parcial, examinando a linha B. A linha B, assim como as células marcadas em amarelo, foi escolhida porque a combinação do número “6” (B7) e do número “1” (B9) deixa a célula B1 sem solução (em branco). Examinando as consequências neste sudoku parcial.

Abaixo uma tabela com as consequências de escolher as combinações possíveis entre B7 e B9.
A combinação da primeira linha da tabela com 2(B7) e 1 (B9) deixa como solução nas células B4 e B6 o número “7”, não pode haver dois números iguais em uma unidade (linha ou QM no caso), o que exclui esta possibilidade.
O mesmo para a opção da terceira linha da tabela com 5 (B7) e 1 (B9), com o número “6” em B1 e 6 (C2) ambos no mesmo QM.
A opção da quarta linha com 5(B7) e 5 (B9) também excluí esta opção (dois números iguais na mesma linha).
A opção da quinta linha com 6 (B7) e 1 (B9) deixa a célula A8 em branco.
As opções da segunda linha com 2 (B7) e 5 (B9) e as opções da última linha com 6 (B7) e 5(B9) são válidas e ambas contêm o número “5” como solução da célula B9.
Conclusão: o número “5” é solução na célula B9.

A técnica pode ser estendida, como no sudoku parcial abaixo. Foram escolhidas as três células em amarelo para ver as combinações possíveis.
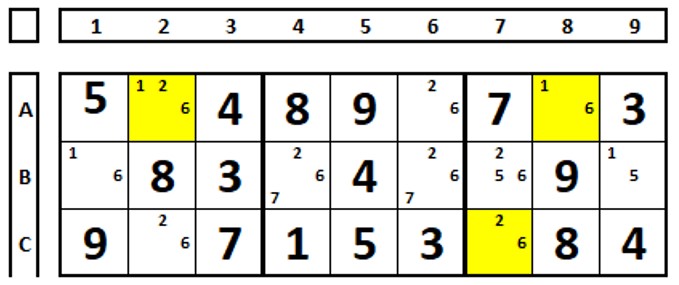
As possibilidades de combinações entre as três células encontram-se nas colunas A2, A8 e C7 abaixo,
Em amarelo as células que apresentam a quebra de regras do sudoku (na mesma UNIDADE não pode haver dois números iguais, uma célula não pode ficar em branco e uma unidade tem que ter todos os números de “1” a “9”). Tente fazer a tabela. As linhas em branco mostram as opções possíveis de combinação das três células. Em todas, B1 = 1 e B9 = 5, logo estes valores são solução destas células.
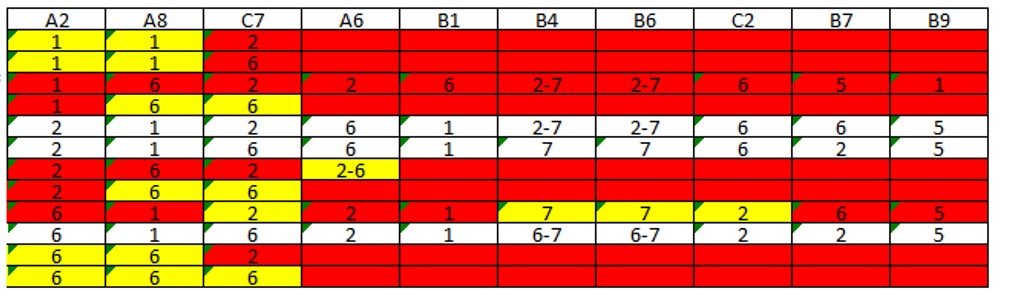
*(linha 3 acima) – Sem solução para o número “6” no QM2
Faça com cuidado as exclusões, muitas vezes ao examinar uma possibilidade pode-se ter associado um XY-Wing, um X-wing, uma Singularidade, entre outros, que permitem ampliar as possibilidades de inclusão/exclusão.
Um último exemplo. Observe o QM5 e o QM7. Ali estão presentes os números “1”, “3”, “5” e “8”. Construindo uma tabela com as duas células marcadas em amarelo: