Forcing chains testa o que ocorre em outras células quando escolhe-se um número ou outro como solução do Sudoku na célula em teste. Nas células alvo pode-se encontrar números que são solução do Sudoku e números que podem ser excluídos. Alguns autores chamam uma regra derivada de “The Dual Forcing Chain” (A corrente de força dupla), que é semelhante, apenas opera com um par bloqueado onde as extremidades enxergam duas célula bi-valor, com o mesmo par de números. No Sudoku parcial abaixo, qualquer escolha na célula A1 força a eliminação do número “A” em C1.
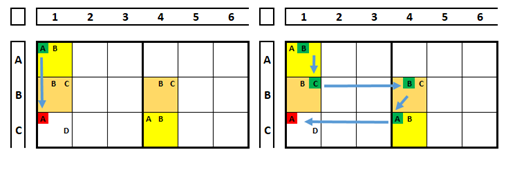
Usando a técnica de coloração para testes verdadeiro e falso. Na célula A5 do sudoku abaixo, o número “2” será a solução ou não desta célula. Examinar as duas situações, usando a cor “verde” para verdadeiro e “vermelho” para falso.
Apesar de não indicar a solução para a célula A5, qualquer escolha excluirá o número “2” da célula B5.
Não é necessário colorir, basta imaginar…
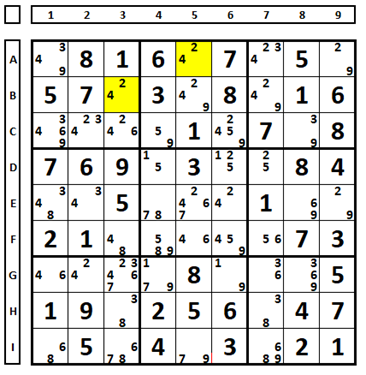
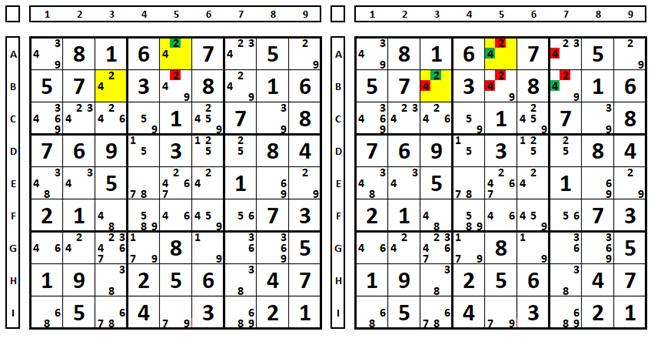
Testando uma célula com três números possíveis. No Sudoku abaixo há três candidatos na célula E7 (números 3, 6 e 8). Examinado o que ocorre considerando cada qual solução do Sudoku:
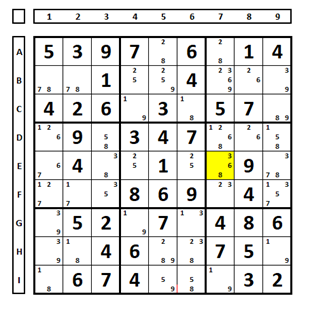
Ao testar cada um dos números, verifica-se que:

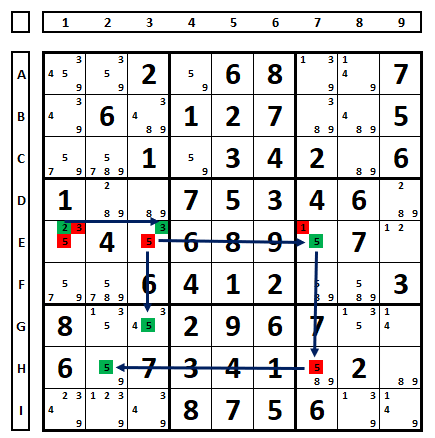
Outro exemplo: a célula B8, independentemente de seu valor, resultará na eliminação do número “8” em B1.
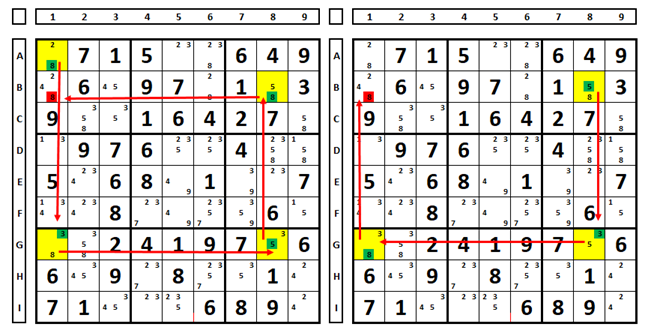
Outro exemplo. A escolha do número “2” em H1 coloca como solução na célula B1 o mesmo número “2”. Como na mesma coluna não pode haver dois números iguais, o número “7” é solução na célula H1.
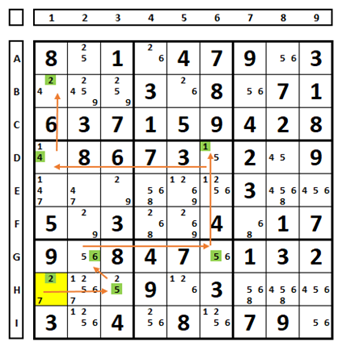
No Sudoku abaixo, o que acontece ao escolher-se o número “2” na célula E1? No QM7 aparecerá dois números “5” como solução para o Sudoku, logo o número “2” em E1 pode ser excluído.