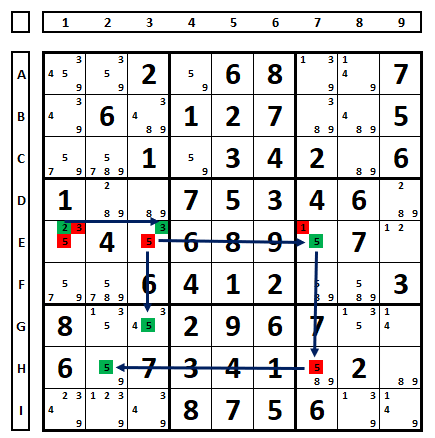
Forcing chains test what happens in other cells when one chooses one number or another as the solution to the Sudoku in the tested cell. In the target cells, one can find numbers that are a solution to the Sudoku and numbers that can be excluded. Some authors call a derived rule “The Dual Forcing Chain,” which is similar, but only operates with a blocked pair where the ends see two bi-value cells with the same pair of numbers. In the partial Sudoku below, any choice in cell A1 forces the elimination of the number “A” in C1.
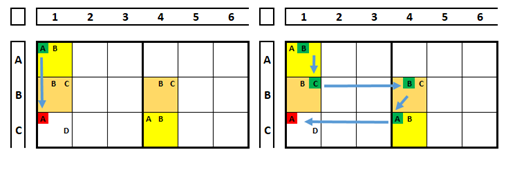
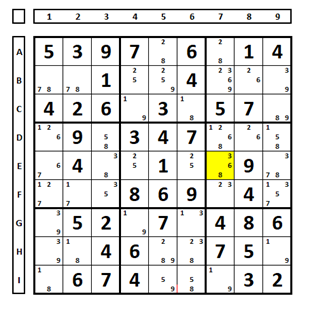
Using the coloring technique for true and false tests. In cell A5 of the sudoku below, the number “2” will be the solution or not for this cell. Examine the two situations, using the color “green” for true and “red” for false.
Despite not indicating the solution for cell A5, any choice will exclude the number “2” from cell B5.
It is not necessary to color, just imagine…
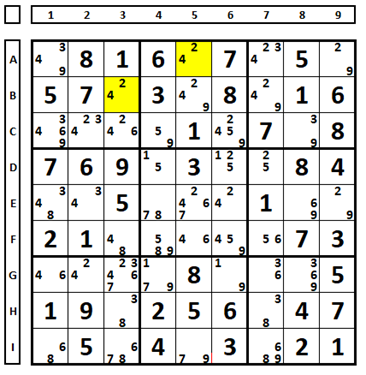
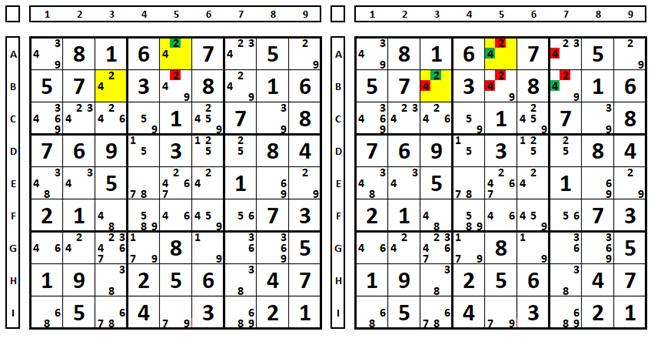
Testing a cell with three possible numbers. In the Sudoku below there are three candidates in cell E7 (numbers 3, 6, and 8). Examining what happens considering each one as the solution to the Sudoku:
Testing each of the numbers, we can verify that:
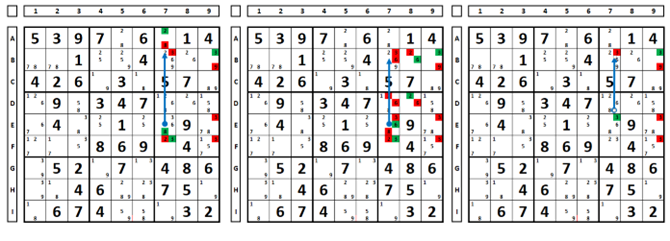
Another example: cell B8, regardless of its value, will result in the elimination of the number “8” in B1.
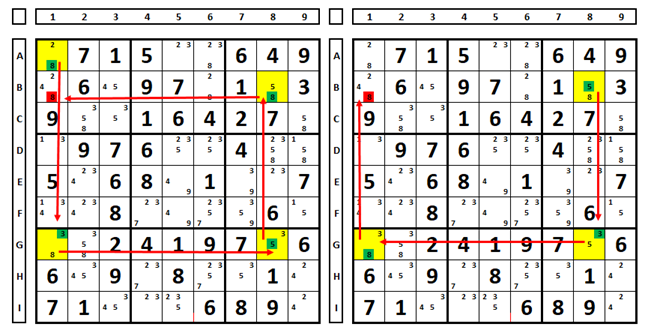
Another example: Choosing the number “2” in H1 results in the number “2” being the solution for cell B1. Since the same number cannot appear twice in the same column, the number “7” is the solution for cell H1.
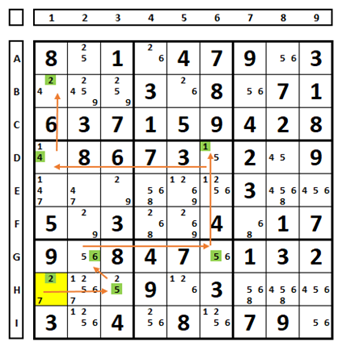
In the Sudoku below, what happens when choosing the number “2” in cell E1? In box 7, two “5” numbers will appear as a solution for the Sudoku, so the number “2” in E1 can be excluded: