Important:
During the course, memorize the technique you stopped at. Restart the course from the home page by clicking on the last technique learned.
What is Sudoku?
Sudoku is a logic game where the numbers 1 to 9 are inserted (without repeating them) in each row and column of a larger square formed by 9 rows and 9 columns. The numbers not only do not repeat in each row or column, but also do not repeat in the same smaller square, which is formed by 3 rows and 3 columns. There are variations in the square format (9×9), which can have a round shape or other geometric figure. There are also those with other formats such as (12×12). But the techniques described here can be used/adapted for these new formats.
Sudoku is a logic game where the numbers 1 to 9 are inserted (without repeating them) in each row and column of a larger square formed by 9 rows and 9 columns. The numbers not only do not repeat in each row or column, but also do not repeat in the same smaller square, which is formed by 3 rows and 3 columns. There are variations in the square format (9×9), which can have a round shape or other geometric figure. There are also those with other formats such as (12×12). But the techniques described here can be used/adapted for these new formats.
Read the definition again, it is essential to understand it for the resolution of any Sudoku.
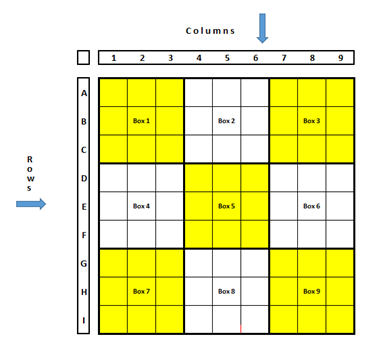
The Sudoku is formed by:
The first cell of the smaller square box 1 will be abbreviated as A1, and so on.
Concept of ‘clue’ and ‘pencil mark’ = ‘candidates’
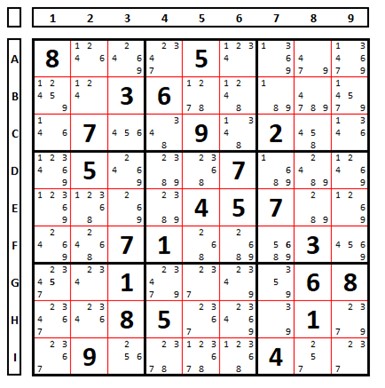
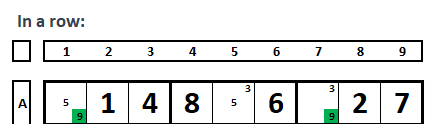
Clues are the numbers that guide the initial placement of numbers in a Sudoku puzzle. In the given Sudoku below, the bolded numbers are the clues (initial formation of the Sudoku), and the various smaller numbers in each cell are the possible numbers that could occupy those cells, which are referred to as pencil marks or candidates.
Concept of “sees”:
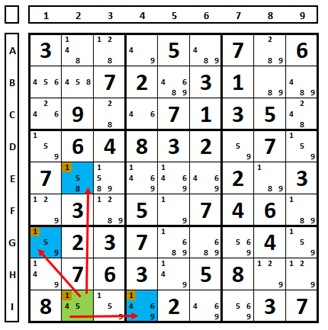
A cell ‘sees’ another when they are in the same row, same column, or same box. In the following Sudoku, the number “1” in cell I2 (highlighted in green) ‘sees’ the number “1” in the cells marked in blue, E2 (same column), I4 (same row), and G1 (same box). To be clear, it also sees the cells H1, A2, and I3 (which contain the number 1). This concept of ‘seeing’ also applies to different numbers, in some techniques, but the concept is the same (row, column, or box). For example, cell I2 is ‘seeing’ cell I7, even though it does not contain the number “1”, because they are in the same row.”
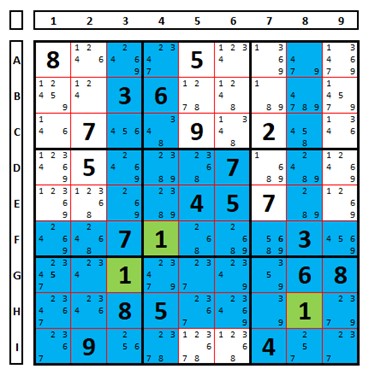
Expanding the concept, each cell ‘sees’ all the other 8 cells in its box, as well as all the other 8 cells in the row and column where it is located. Cell C7 (highlighted in green) ‘sees’ all the cells marked in blue. And these positions (the blue cells) are ones where, by the rule, the number “2” will not appear.
The concept is important because it shows us the possible positions of a certain number, such as the number “1” in the example below, which will be in some of the “white” cells, except for the given clues (for example, the number “8” in cell A1 is a clue and the number “1” cannot occupy that cell).

Conjugate pairs:
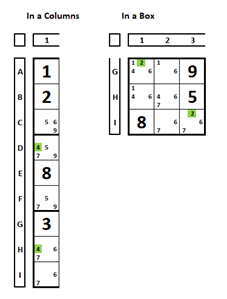
Pairs of “unique” candidates in a unit. In row A, the number “9” is only present in cells A1 and A7.
In column 1, the number “4” is only present in cells D1 and H1.
In the box, the number “2” is only present in cells G1 and I3.
Unique solution:
Sodokus must have a unique solution. Those that allow for more than one solution are poorly designed (including the solving techniques presented in this or other books or websites, which may contain errors for these sodokus). However, fortunately, they are difficult to find in quality publications.
Concept of Unit or Unity:
In the context of a Sudoku puzzle,it refer to a specific part of the puzzle, such as a row, column, or 3×3 square (box)
Concept of Chain:
A chain, or a strand, is a relationship that can be established between the numbers that make up the cells in a Sudoku puzzle. It consists of links that jump from one cell to another, following certain rules. In the example below, there is a relationship between the bi-value cells (2/4) that make up this Sudoku. When a number (2 or 4) is the solution for one cell, it will also solve the value for all other cells in the chain.
In the case below, cells H2 and E8 are the endpoints (the beginning and the end) of this chain.

Bi-value cells are cells with two candidates, and only one of the two “candidates” will be the solution for that cell.
There may be more than one chain/strand in a Sudoku puzzle. The implications of this will be shown in the techniques ahead.
The next concepts will be seen in detail when techniques use them. Read them without worry at this moment.
Concept of links:
String Links:
When there is a relationship within a UNIT: if A, then not B, or vice versa. In the example below, the strong links are A1/A8, A1/B3, and B3/B5. In the case of A1/A8, if the candidate “4” is chosen in A1, then the number “2” will be the solution in A8, and vice versa.
In the context of Sudoku, strong links refer to a relationship between two cells where the solution to one cell determines the solution to the other cell.

Weak links:
In the context of Sudoku, weak links refer to a relationship between two cells where the solution for one cell does not necessarily determine the solution for the other cell, but may eventually eliminate one or more candidates.
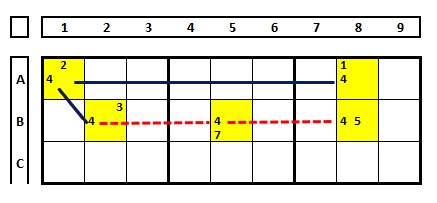
There is no certainty about the influence of a “4” on the other in row B.
Having one of them as “false” doesn’t indicate which of the other two is true. Cell B2 (or B5) is not in the same UNIT as cell A8. Be careful, it is not possible to create links between them.
On the website, solid blue lines are used for strong links, and solid or dashed red lines are used for weak links.
Group links:
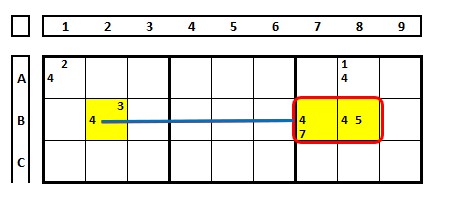
In Sudoku, group links refer to a relationship between a group of cells (in a row, column, or 3×3 box) where a certain candidate can only appear in those cells. This means that if that candidate is solved for one cell in the group, it can be eliminated as a candidate from all other cells in that group.
In the example below, there is a strong inference between B2 and the set B7/B8. Either the solution for the number “4” is in one or the other. Therefore, a strong link unites them. Note that there will be a weak link between B7 and B8, due to the presence of the number “4” in B2 or A8. But, observe that there is a strong link between A8 and the set B7/B8.
Don’t worry about the links for now, they will be discussed later.
Notation:
N = number of cells
N+x = Number of candidates in the cell
Example:
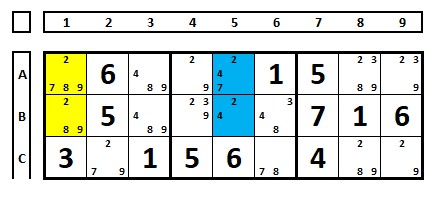
Notation of cells marked in yellow: N=2 (2 cells) and N+x = N+2 (4 possibilities: 2, 7, 8, 9).
Notation of cells marked in blue: N=2 (2 cells) and N+x = N+1 (3 possibilities: 2, 4, 7).
This notation will be used in some techniques.
If the notation is “N+3”, it means that the number of cells is “N” and the number of candidates in the set of cells is “N+3“.
Don’t worry about this now.
Hint:
To train your reasoning skills, first try to fill in the cells (intersection of a row and a column) without putting in the possible “candidates” in the cells (pencil marks).
That is, at the beginning of the solution, train your memory and reasoning. For example, in the Sudoku below:
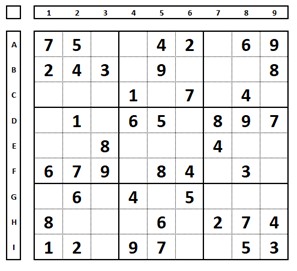
Do not do this (putting pencil marks – or candidates – that could occupy the cells for guidance):

The reader will quickly realize (with little training) that the number “1” can only occupy cell A3, since it cannot, by definition, occupy cells C1, C2, and C3 (same row, there can only be one “1” in this row and it already occupies cell C4). Similarly, the number “4” can only occupy (in box 7) cell I3. The number “5”, in box 2, cell B4, and so on.
Exercise: Try to solve this Sudoku without putting pencil markings in each cell (as was done in Box 1).
Techniques for solving Sudoku.
In the demonstration of the techniques, more experienced individuals could deduce (identify beforehand) the location of the solutions in some cells, but this is not done here for didactic purposes. The techniques are taught in increasing order of difficulty (although they do not present greater difficulties for understanding). It is recommended to follow the order presented on this website, which generally corresponds to the order presented by several authors.

