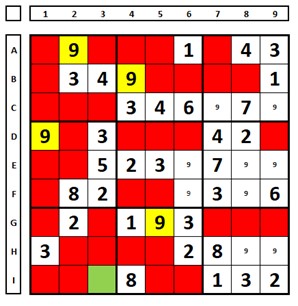
Different from the Hidden Single, only a specific number can occupy a cell because the other eight numbers can “see” this cell.
In the example below, only the number “9” can occupy the cell marked in green. Examine the numbers in row C, column 4, and box 2 to verify that the other numbers (1, 2, 3, 4, 5, 6, 7, and 8) can “see” cell C4:
Below is presented an extra content, taking advantage of what has been learned so far.
Visualizing possibilities for the location of a certain number.
Intersection of a box, a row, and a column.
One can eliminate (in red below) a candidate in various cells and check the cells where this number is a candidate (in green below):
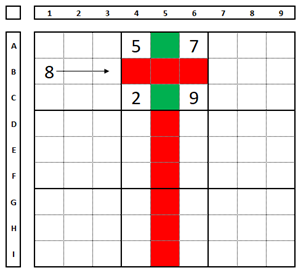
Since the number “8” can only be in box 2 at position A5 or C5, it cannot be a candidate in the other positions marked in red in column 5.
Comparing boxes, rows, and columns
Watch the sudoku below: In box 4, the only possibility for placing the number “3” as a candidate is in the positions marked with the lowercase number “3” (column 1, cells D1, E1, and F1). Therefore, the number “3” cannot occupy column 1 in box 1.
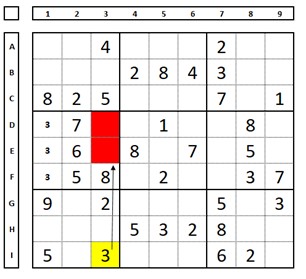
With this information, we can locate the number “3” in box 1:
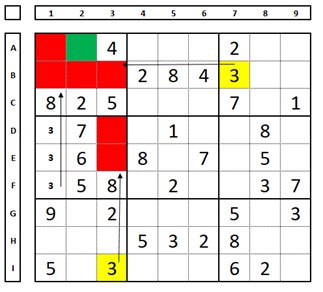
Another example. The number “1” can only be in cell I7:
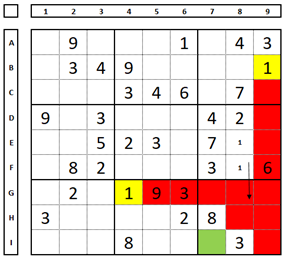
Another example. In row I, the number “9” can only occupy the cell I3 (the only cell in this row that can receive this number). Note that the number “9” can only occupy cell C7, as it is the only possibility in column 7. Examine this example, as it is a little more complex, but very didactic:
(The numbers “9” in the yellow cells are “clues” given by the author of the Sudoku. The cells marked in red are the positions that this number cannot occupy. The numbers “9” in small size – i.e. pencil marks – are the possible positions that this number can occupy).