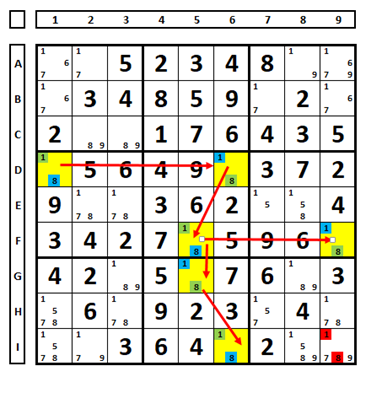
Also called in English ‘XY/RP chain’.
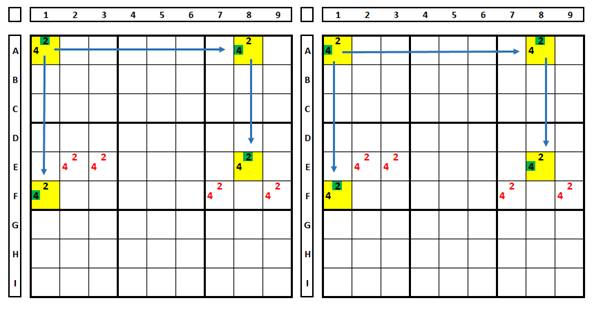
Where X and Y are the same two numbers that make up bi-value cells forming pairs. In the example below, there are pairs formed by the yellow cells for numbers X=2 and Y=4.
For any choice in cell A1 (2 or 4), the end cells of the chain will always have opposite numbers, so the numbers ‘2 and 4’ will not be in the positions marked in red, which are the cells that ‘see’ both endpoints.
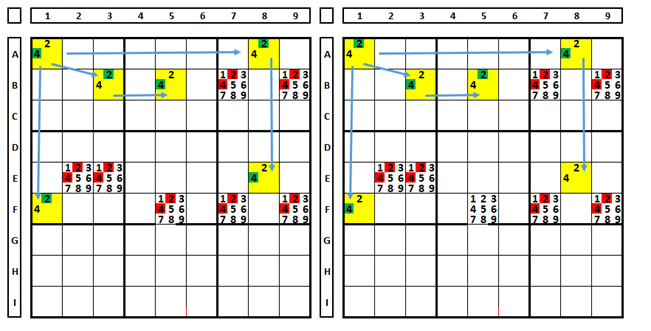
Expanding, adding one more remote pair. In the Sudoku below, the existence of one more remote pair allowed for the exclusions of numbers in other cells to be expanded.
In summary, in this technique (XY-RP chain), an even number of bi-value cells is necessary (in the first example, 4 cells, in the second, 6 cells) so that the initial and final numbers of the chain are antagonistic.
If cell B5 did not have the remote pair (2/4), cell B3 could not be used for the solution because we would not have an even number of cells (but five). However, the existence of the 5th cell would not prevent the use of the other 4 (or expanding, the odd number of cells does not prevent the use of existing pairs, provided that the branching is not unique – it continues).
Note that the eliminated numbers “see” the end of each “Branch.
Also note that even if the RP chain is long (as in the second case above, with six cells), it is possible to partially use the pairs, as was done with the branches A1/F1/A8/E8 (which allowed exclusions in cells E2/E3/F7/F9) and A1/A8/B3/B5 (which allowed the exclusion in B7/B9 – in blue).
The chains must be “branched”. Situations where pairs are formed from a single cell do not allow elimination conclusions:
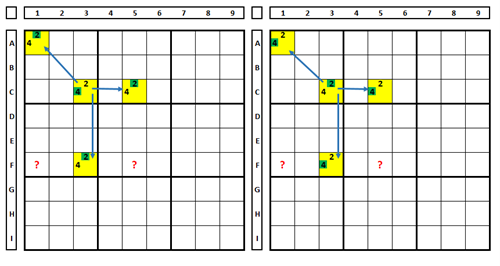
Depending on the choice made in cell A1, either the number “2” or “4” will be excluded from cells F1/F5. Since the solution value in A1 is unknown, no exclusions can be made.
There are interesting cases, such as the Sudoku below, seen in the colorimetric method, where even chains (D1, D6, F5, F9) meet odd chains (D1, D6, F5, G5, I6), starting from the same cell (D1). Using the colorimetric method, we can exclude the numbers seen by both ends (in red).