Recently a very interesting new technique was published at (https://kzblow.info/clone/brand-new/k3_Fxq6dpsqIrJo.html).
Invariant 1:
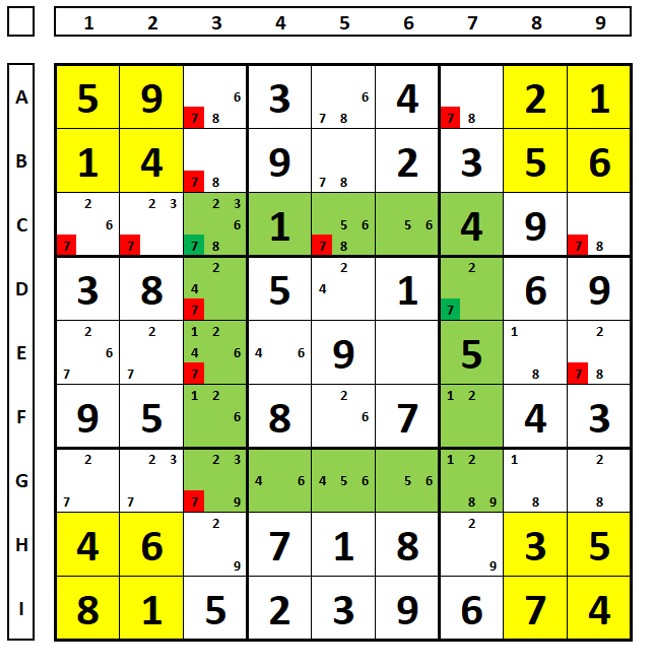
In all sudokus, the following happens, let’s go straight to an example. In the yellow regions, there are numbers 1, 2, 3, 4, 5, 7, 8, 9.
There is no number “6”.
The same happens in the blue region. All nine numbers could appear.
The important thing is that each number appears the same number of times in the yellow and blue cells.

Outro exemplo. Todos os números (de 1 a 9) estão contemplados nos dois conjuntos.
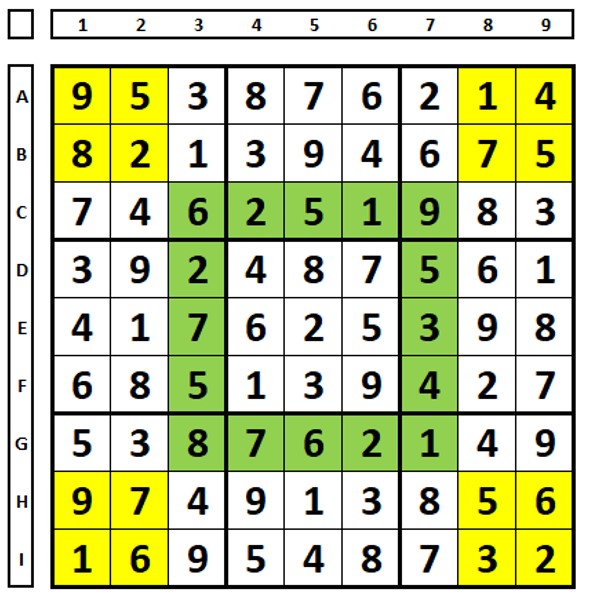
Em que se pode usar a informação dada? Um exemplo.
In the Sudoku below, the number “8” marked in blue (cell B8) can only be in one of the cells E3 or G4, or in both (since it can be at most in I1 as well). Thus, there is a strong link between these two cells, as has never been seen before in this site. Let’s try an X-Cycle?
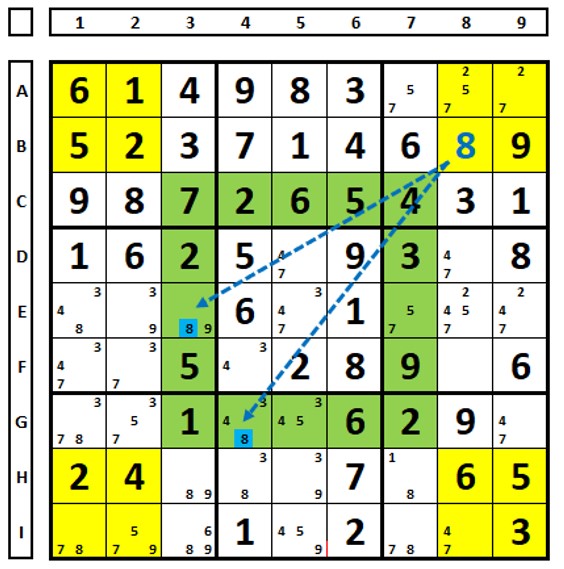
Link in green (strong link transformed into weak link). Knowing the position of the two “8” numbers allowed the construction of this X-cycle and the exclusions shown.
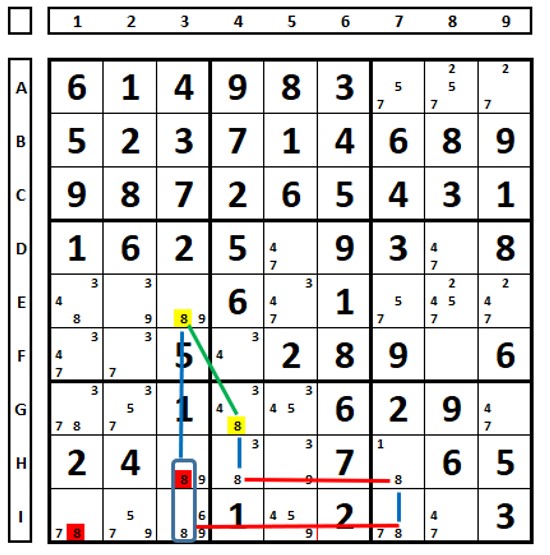
In the Sudoku below, the number “8” is not present in the yellow sets as a clue or a candidate, so it can be excluded from the positions marked in red:
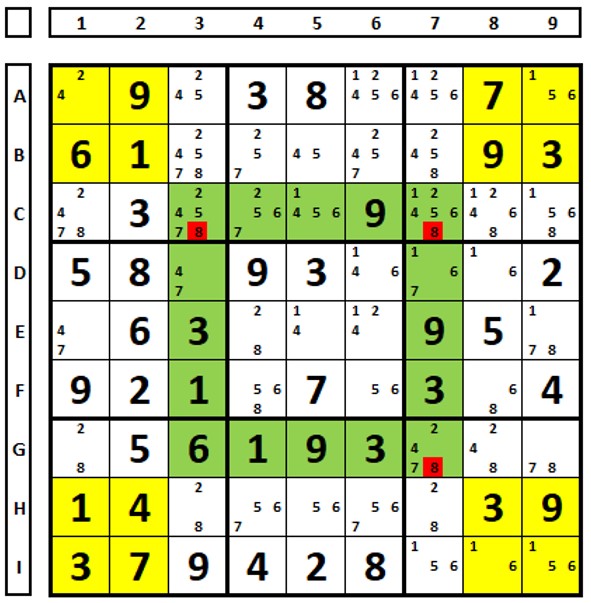
In the Sudoku below, there are two “3” numbers in the green set. In the yellow set, there will be one “3” in the blue set and one in the gray set, completing the two necessary to match the green set. The “3” in cell H2 can be excluded.
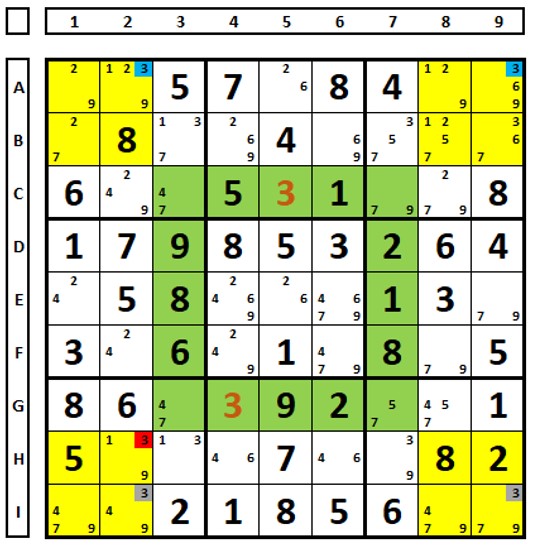
In the Sudoku below, there is only the number “2” in the yellow set in cell A8, therefore there will only be a number “2” in the light blue set. Only number “2” in cell D7 or cell G4 will be solution for sudoku. Both see this number in cell D4, and it can be deleted there.
Invariant 2:
There are the same numbers (with the same candidates) in the green and blue areas. Here’s an example: the green set has the same numbers repeated in the same way in the blue set.

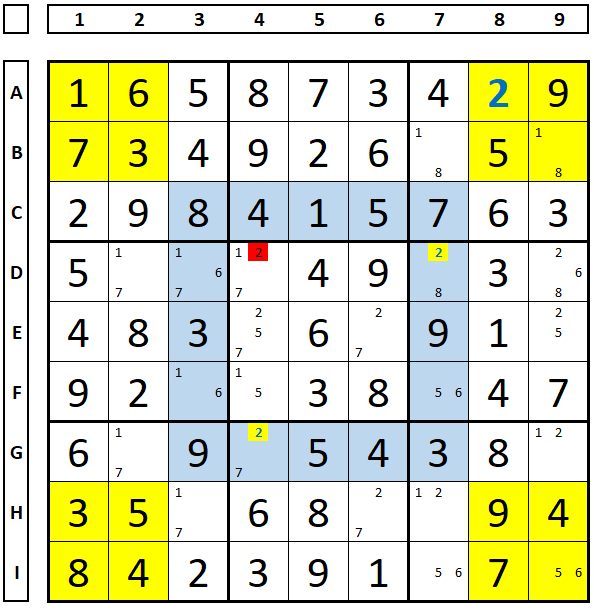
In the Sudoku below, the blue region has two “3” as the only solution in this set (B4 and I5) and there are no candidates in any other blue cells. Therefore, in the green set, there can only be two “3”. One is already fixed in cell G9, so it can only be in one of the marked positions (E2 and F2), and can be excluded from A2.
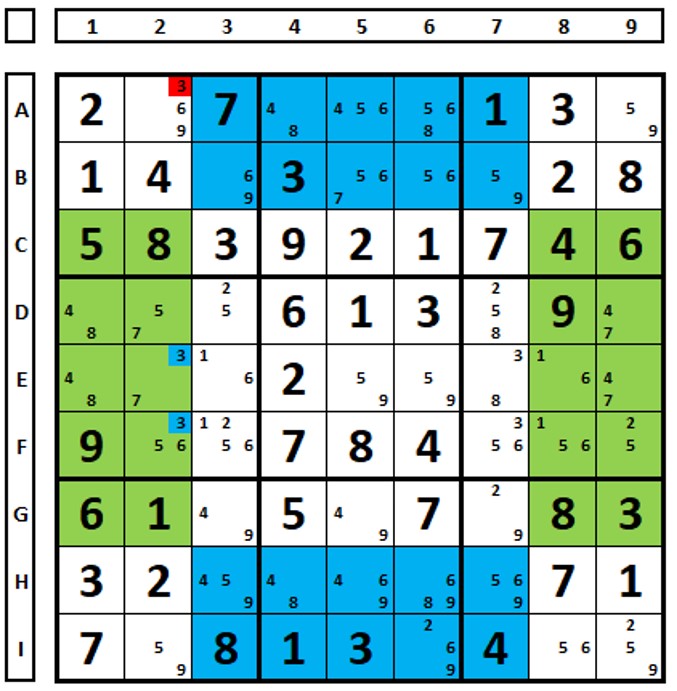
In the Sudoku below, in the yellow set, the number “3” is in the two brown marked positions (there are two). In the green set, it is in cell B3 and necessarily in cell A7. The number “3” in A8 can be eliminated. Remember, several techniques can lead to the same conclusion, the number “3” in cell H8 would make the same exclusion.
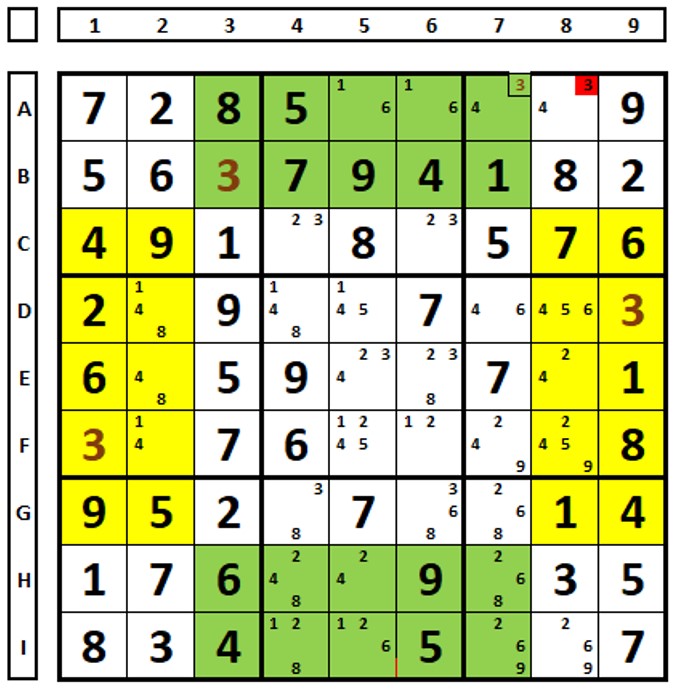
In the Sudoku below, the green sets must have four “3” numbers. Therefore, the yellow sets will also have four “3” numbers. The number “3” in cell C8 is the solution for this cell.

In the Sudoku below, the number “5” appears in two positions in the yellow set as clues (cells D1 and F8), and it may also be in a third position (cell C9). Therefore, there must be two “5” numbers in the green set, with the possibility of a third. However, upon observing the green set, there is only the possibility of placing one more “5” number (in addition to the “5” number in cell B3), either in row A or row I. By looking at the “5” number in cell A4 and solving the Sudoku accordingly, the following situation arises:

In the Sudoku below, the number “4” appears only once in the yellow set (once as a “clue” in cell E2, and not as a candidate in the other yellow cells). Therefore, it can only appear once in the green set (in cell A4), which means that the candidate in H3 must be excluded.

In the sudoku below the number “7” appears only once in the yellow set (in cell I8). Looking at the green set, choosing the number “7” in cell C3 makes this number a solution in cell D7, which goes against the rule (in this case there can only be one number “7” in the green set), so it can be deleted from cell C3. This does not mean that the numbers marked in red are not some of them sudoku solutions.