It is characterized by a box (3×3), where four cells (or more) do not contain the candidate, leaving a pattern with the candidate in the form of L, T or +, called a hinge. The cells must see a blocked pair (of the same number) in a row or column outside the box. With this it is possible to exclude a candidate that sees the ends of the two sets.
In the example below, in box 9, cells G7, G8, H7 and H8 form the empty rectangle (there is no number “7”) and the L (inverted). If any of the numbers “7” in cells G9 and I9 is a sudoku solution, they see the end of the blocked pair (A1/A9) in line A, then this number in cell A1 is the sudoku solution, allowing to eliminate this number in cell I1. If this number in cell I7 is the solution, this also excludes this number in cell I1.
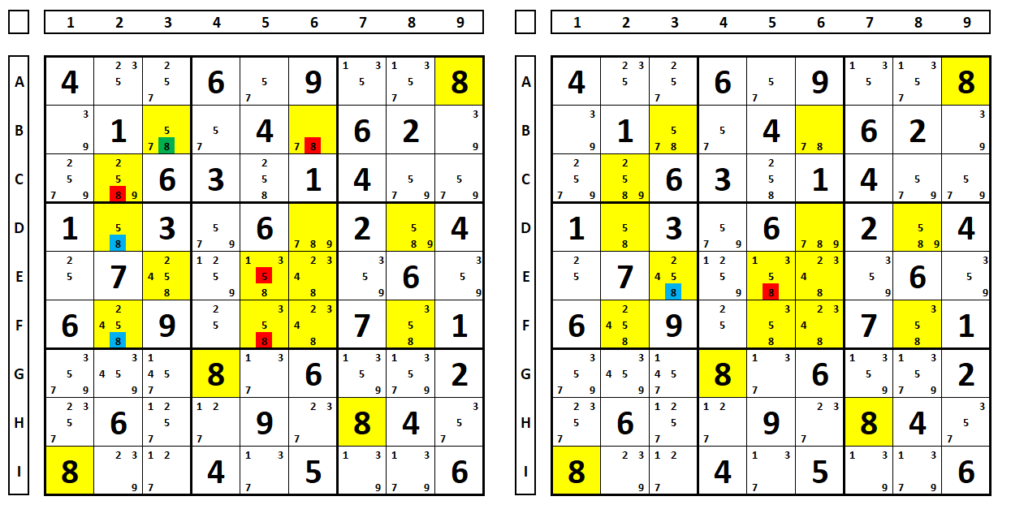
Another example in “L“: any choice for the number “8” in C1 or G1 will result in the number “8” in G7 being excluded.
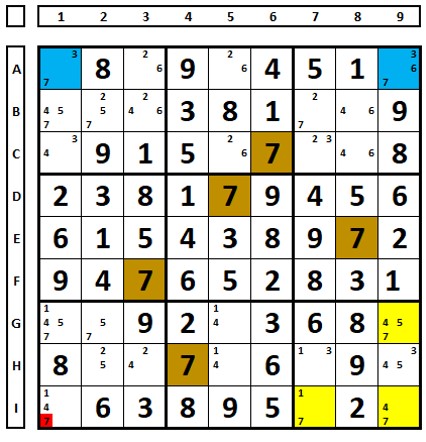
An example of “T“: for any choice of the number “7” in the blue cells, it will be excluded in B4.
Example with “+”: for the number “5”, any choice in the green cells will exclude this number in cell B3.
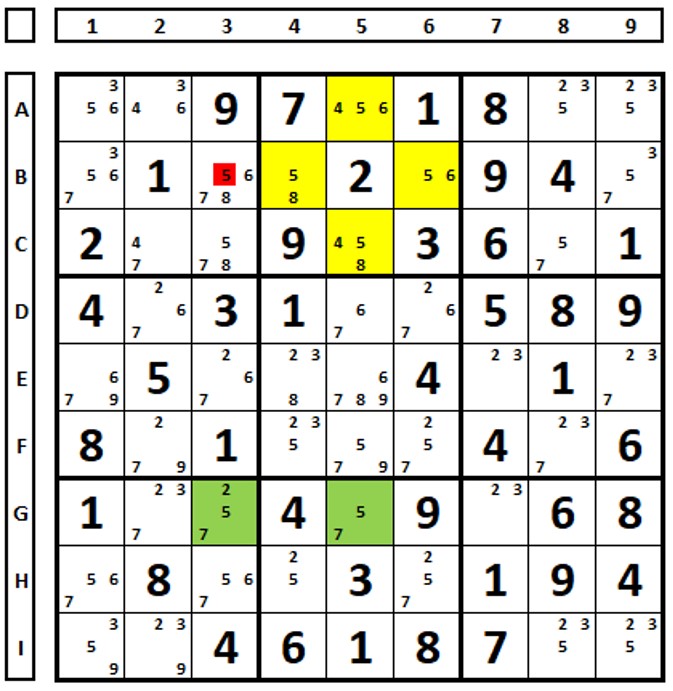
In the Sudoku below it is possible to eliminate the two numbers “4” marked in red. There are two ERs here. Try.
Many times when trying to solve Sudoku using a certain technique, it doesn't work, so check if there are no other conclusions to be drawn, let's call this "extra-technical tip".
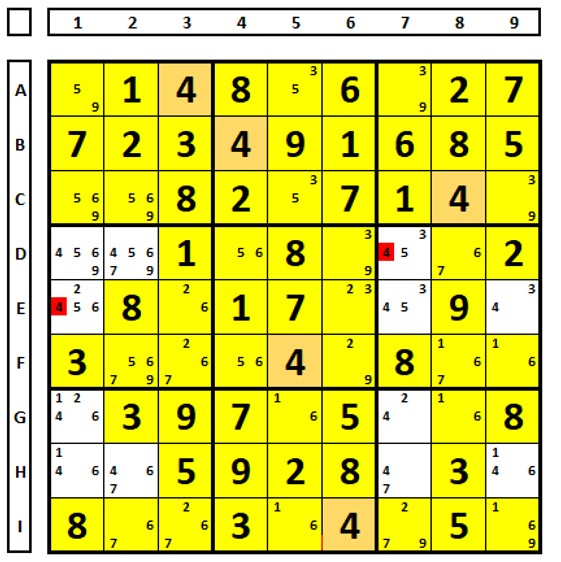
Paying attention to possibilities, based on known techniques, allows for excluding/including numbers in certain cells. Examining the Sudoku below, for the number “9”:

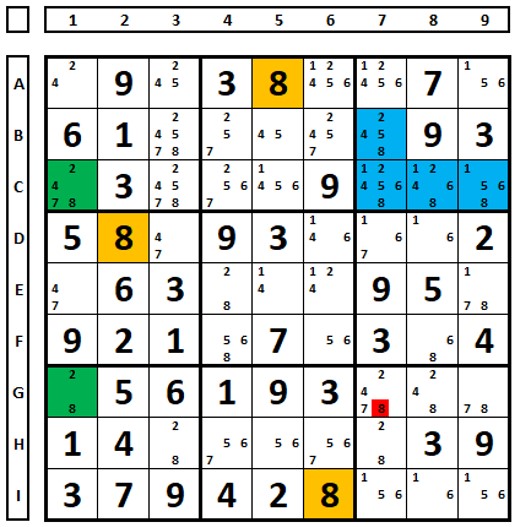
It is possible to see a situation “similar” to ER. The cells marked in blue in box 3 do not form an ER. What happens when they “see” cells marked in yellow? By choosing the number “9” in A2 or H2, the situations below occur. The green positions in boxes 3, 6, and 9 show the possible positions of this number. The number “9” can be excluded in cell C9 by this observation.
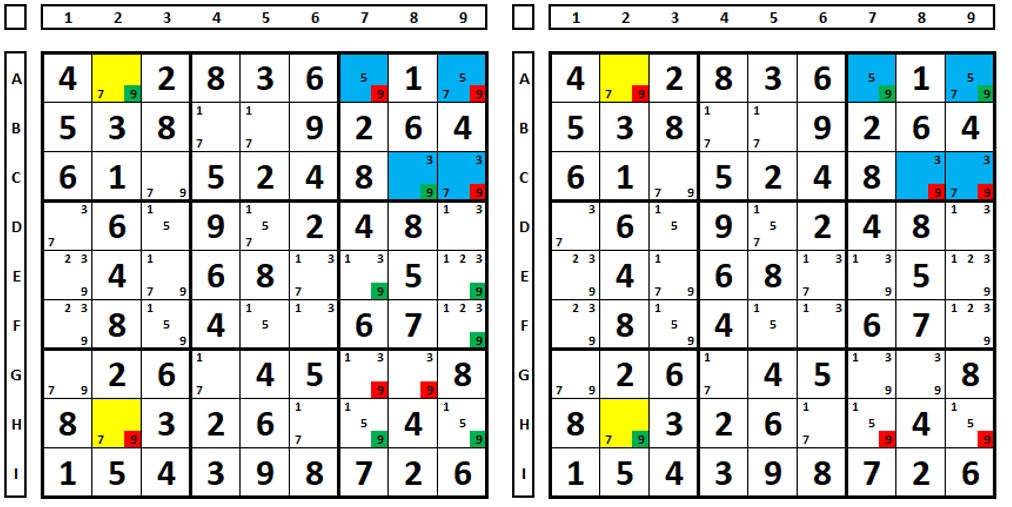
Repeating. One should always be on the lookout for similar situations. In this same sudoku puzzle, examining the number “6”. There is a fake ER (not really fake) between the green and blue marked cells, but what happens when you consider an ER and test?

When choosing cell D4 and then D9 as the sudoku solution, it is verified that the numbers “6” are common for elimination in D1, D2, F2 and F3.
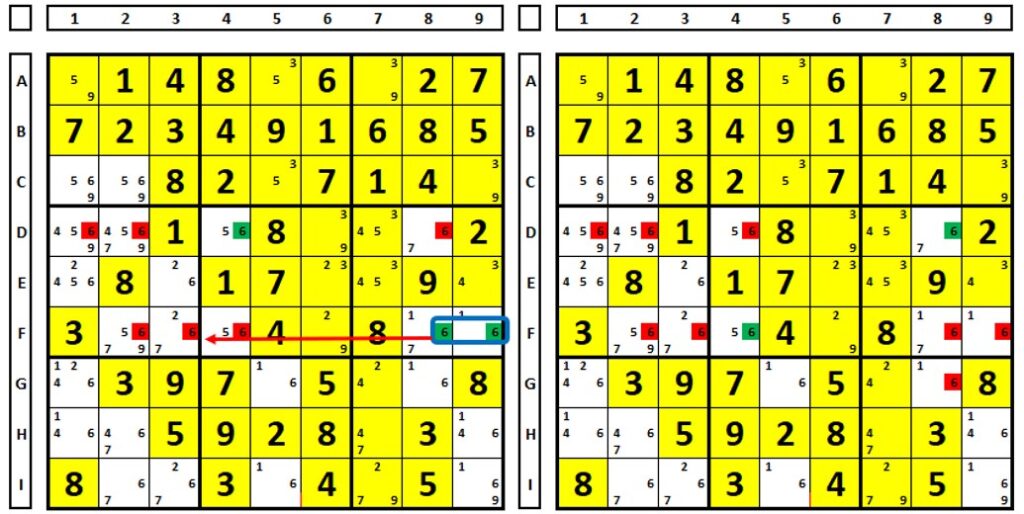
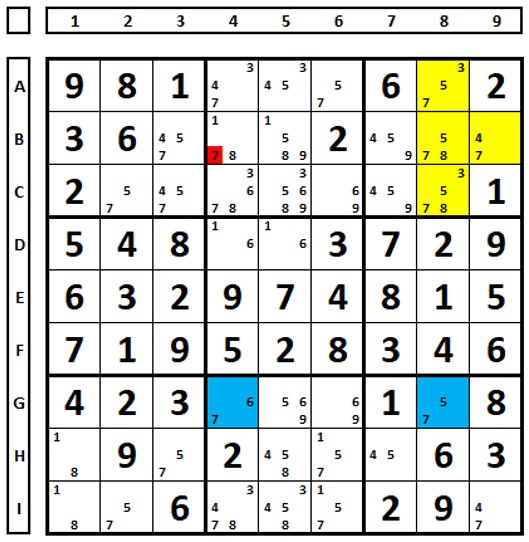
In the example below, for the number “8”. In box 4 there are two cells (D2 and F2) directed to two cells in yellow in box 1 (left figure). If one of the two is a solution to this sudoku, there will be eliminations in red. If cell E3 is a solution (right figure), there will be eliminations in red. Common elimination (D5) can be performed.