Normalmente o autor do Sudoku deixa como pista no Sudoku original os números que evitam a existência de “singularidades”. Quando o autor do Sudoku não dá uma pista o “retângulo evitável” deve ser evitado, pois levará a um Sudoku a ter duas soluções ou nenhuma.
Direto a um exemplo. O Retângulo único ou Retângulo Evitável são as quatro células marcadas em amarelo, todas com somente os mesmos dois candidatos (quatro células bi-valor, com os mesmos candidatos, em somente dois QMs).
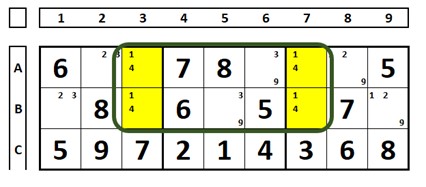
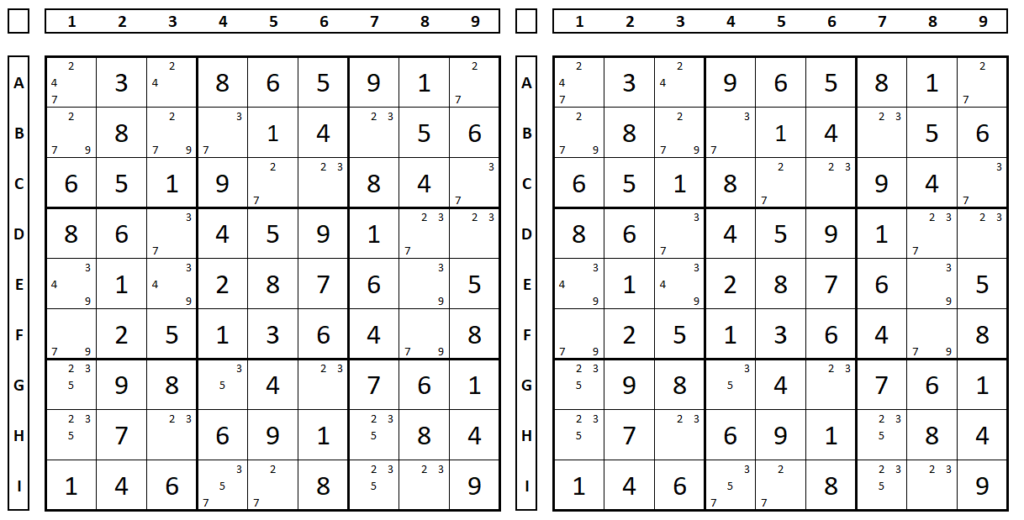
Para estender a explicação observe o sudoku abaixo. O autor, no Sudoku original, fixou em negrito as pistas, em especial os números “8” e “9” (nas células A4 e A7), para que o Sudoku tivesse uma só solução. Os números em itálico foram descobertos durante a solução do sudoku. Inverta as posições deles e terás outro Sudoku válido. Reforçando, este Sudoku tem somente uma solução porque o autor fixou os números “8” e “9”. Se os números “8” e “9” nas células A4 e A7 tivessem sido resolvidos pelo leitor (e não fixados pelo autor) o Sudoku teria duas soluções.

Caso o autor do sudoku não tivesse dado como pistas os números “8” e “9” (células A4 e A7)o sudoku teria as duas soluções abaixo, sendo um sudoku de má qualidade (que são raros nas boas publicações) e poderia não ter solução ou algumas técnicas poderiam conduzir a erros.
A técnica usa somente dois QMs.
Os QMs não precisam ser contíguos, mas somente pode-se usar dois QMs. No modelo abaixo, as células em amarelo, azul ou verde são exemplos de onde pode-se verificar a existência de singularidade.
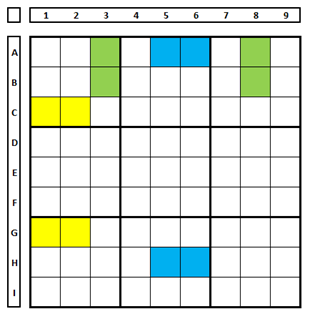
Demonstrando o engano com o uso de quatro QMs.
Aparentemente o número “4” estará obrigatoriamente em B9 se aplicada a regra da singularidade, mas isto não é correto, a solução desta célula é o número “5”.
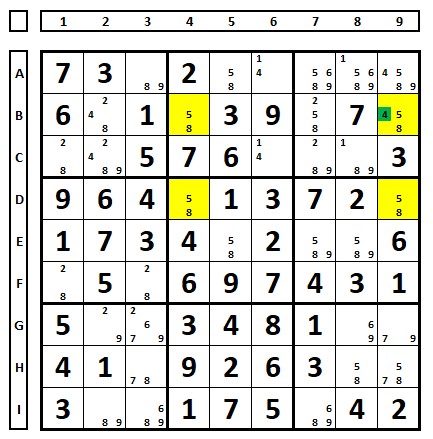
Abaixo o Sudoku resolvido. A inversão 8/5 não traz um segundo sudoku, já que o Sudoku da direita é invalido (dois números “8” no QM 5). Demonstrado porque nesta técnica deve-se usar somente dois QMs.

Dica: esta técnica só funciona para Sudokus bem construídos, com apenas uma solução, mas este é o caso da quase totalidade dos Sudokus publicados em revistas e jornais, por isto não se preocupe e use a técnica, que resolve muitos Sudokus com dificuldade média.
Releia os conceitos acima para entender bem a técnica, que dá solução em muitas células de muitos sudokus.
Retângulo evitável exemplo 1:
No Sudoku abaixo os números em negrito formam o Sudoku original, “pistas” dadas pelo autor. Os números em Itálico/não negrito foram descobertos na solução do Sudoku.
As posições em amarelo mostram um retângulo que deve ser evitado – sem uso de pistas, pois se o número “5” em E7 fosse parte da solução, teríamos o Sudoku com duas soluções, logo o número “5” em E7 pode ser excluído.
Explicando melhor, quando o Sudoku fosse resolvido, com o número “5” em E7, o Sudoku teria duas soluções (os números “9” e “5” poderiam um ocupar a posição do outro gerando outro sudoku). Como os sudokus de qualidade devem ter somente uma solução, o número “5” em E7 deve ser excluído.
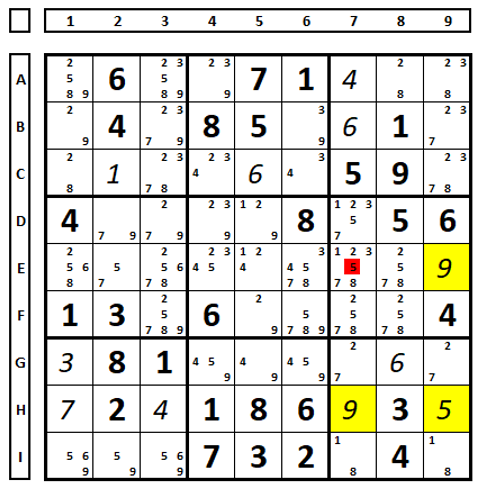
Observe que mais duas técnicas estão eliminando o número “5” em E7. A primeira é o número “5” em D7. A segunda é que os números “1” e “3” ocupam somente as células D7 e E7 no QM 6, podendo os demais candidatos nestas células serem excluídos.
Retângulo evitável exemplo 2:
Se houver apenas uma célula no retângulo que contenha candidatos extras, os candidatos comuns poderão ser eliminados dessa célula. No caso abaixo, o número “7” será solução em H7.
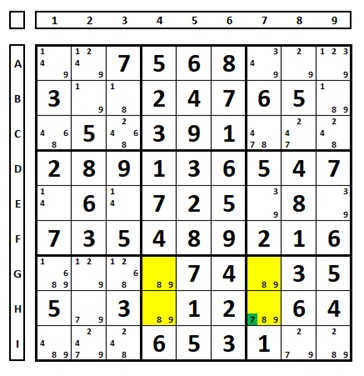
Retângulo evitável exemplo 3:
Na linha ou coluna do retângulo há o mesmo número extra que não consta na outra linha/coluna. Este número pode ser excluído da célula que enxerga ambos os números. Não se sabe, neste momento qual dos números “9” será solução (A2 ou A3) mas um será para evitar a singularidade.

No sudoku abaixo, há a possibilidade de haver singularidade nas células marcadas na cor amarela. Nas células E5 e E6, o número “9” será solução em uma das células, o que impede o número “3” ser solução em qualquer uma destas células, por consequência, o candidato “3” na célula E4 faz parte da solução deste sudoku.

Retângulo evitável exemplo 4:
Um retângulo formado por duas células contendo somente dois números possíveis (A e B) em uma linha/coluna. Na outra linha/coluna há números extras, mas um dos dois números (A ou B) que compõem o retângulo são exclusivos desta linha/coluna, o outro número do retângulo pode ser excluído.
No exemplo abaixo haverá duas exclusões. O número “2” encontra-se na coluna 4 somente nas células marcadas em amarelo, e será solução em uma destas células, neste caso, para que não ocorra singularidade o número” 8” deve ser excluído de ambas as células.

No Sudoku a abaixo, qualquer escolha que se faça do número “3” em E2 ou H2, força o número “1”, com isto, os números “3” em azul devem ser excluídos para evitar-se a singularidade.
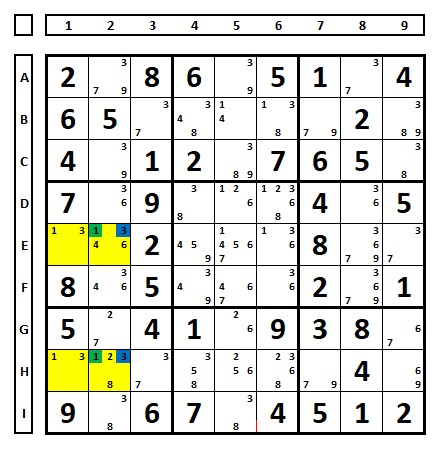
Retângulo evitável exemplo 5:
Este é para pensar! Observando o exemplo abaixo, há a possibilidade de singularidade nas células marcadas em amarelo (7,3). Caso isto ocorra (as quatro células com estes dois candidatos, haveria singularidade).
Observe que, se a solução nas células A8 e A9 for (5 e 8), não importando em quais das duas células se encontram, haverá as eliminações em vermelho, criando-se a singularidade.

Logo, a solução em A8 ou A9 será o númeo “3”, sem saber-se em qual das duas, mas permite as seguintes conclusões:

Retângulo evitável exemplo 6:
Este é um teste de singularidade que utiliza duas células, no mesmo QM (na mesma linha ou coluna), com dois candidatos. Ou seja, um Naked Pair. Em outro QM encontra-se os mesmos dois candidatos, com candidatos extras.
Direto a um exemplo. No Sudoku abaixo há um Naked Pair nas células E4 e E5, e a possibilidade da formação de singularidade com as células H4 e H5. A técnica consiste em “deletar” temporariamente os candidatos números “2” e”4” das células H4 e H5 e ver se forma um Naked Pair, Naked Triple ou Naked Quads naquele QM.

Fazendo a eliminação temporária abaixo dos números “2” e “4” em H4 e H5. Forma-se um Naked Pair nas células marcadas em amarelo (os números “1” e “3”, dois números em duas células), dentro do mesmo QM. Com isto, os candidatos em vermelho, dentro do QM, podem ser excluídos (não esqueça, no sudoku acima).

Outro exemplo. No Sudoku da esquerda há possibilidade da formação de singularidade nas células marcada em amarelo. Foi realizado um teste no Sudoku da direita, com a eliminação temporária dos números “2” e “6” das células F4 e F6, formando um Naked Quads, nas células marcadas em amarelo (4 células, 4 números, no mesmo QM). Com isto pode-se eliminar os números “2” e “3” (que são do Naked Quads) da célula D5, que não pertence ao Naked Quads. Lembre-se, nunca elimine um número que faça parte da singularidade (ou seja os números “2” e “3” das células F4 e F6 neste caso) e a eliminação é no sudoku original (neste caso o da esquerda).
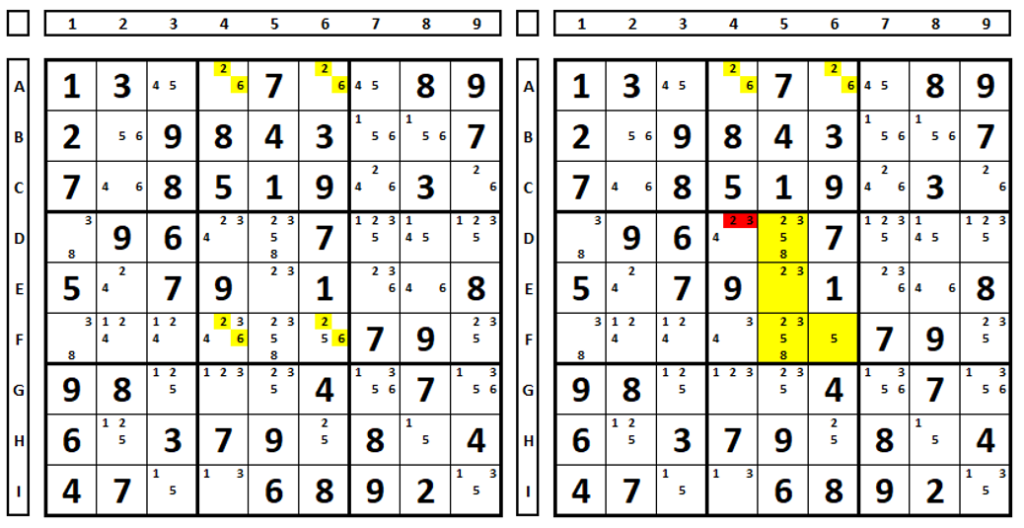
A técnica não funciona quando há possibilidade de haver duas ou três soluções de Naked no QM. Examinando um exemplo. No Sudoku da esquerda há a possibilidade de existir singularidade nas células marcadas em amarelo (números 1 e 9). Ao fazer seu espelho a direita eliminando os números “1” e “9” nas células A1 e C1 temos dois Naked Pairs (A1/A2 e A1/C1), além disto um Naked Triple (A1/A2 e C1). Usando a técnica aparentemente todos os números “9” das células B3/C2/C3 seriam excluídos, mas este número é solução na célula B3.

Retângulo evitável exemplo 7:
Também chamado Unique Hidden Rectangle ou Retangulo Único Oculto. Indo diretamente para o exemplo. Este tipo de singularidade ocorre quando o retângulo (em amarelo) possui dois candidatos extras (no caso os números “8” na célula C7 e “3” na célula F8). A condição é que o outro número (o “7” no exemplo) só ocorra dentro do retângulo que forma a singularidade. Observe que o número “7” forma um X-Wing, a solução de um levará a solução dos demais. Caso os dois números “7” dos conjuntos que contém os candidatos extras fossem escolhidos ter-se-ia a formação da singularidade (faça o teste), por este motivo os dois devem ser excluídos.

Retângulo evitável exemplo 8:
É necessário um retângulo com duas ou três células com candidatos adicionais. Olhe a célula bi-valor e verifique o canto oposto do retângulo. Se um candidato da singularidade não enxergar nenhum outro a não ser dentro do retângulo, o número oposto pode ser excluído.
Ou, ocorre quando os números em um retângulo enxergam candidatos extras fora do retângulo, a exceção de um. Se um dos números componentes do retângulo (A e B) somente puder existir numa linha e coluna do retângulo, o outro número do retângulo (A ou B) pode excluído desta célula. No exemplo abaixo o número “6”. A célula H7 enxerga a oposta célula F8. O número “6” na célula F8 somente enxerga outros “6” dentro do retângulo evitável. Logo o número “1” pode ser excluído em F8.

Examine este exemplo:

Retângulo evitável exemplo 9:
No exemplo abaixo, caso o número “1” da célula I5 fosse a solução da célula, haveria a criação de singularidade nas células amarelas. Neste caso, a solução é o número “8” marcado em azul da mesma célula.
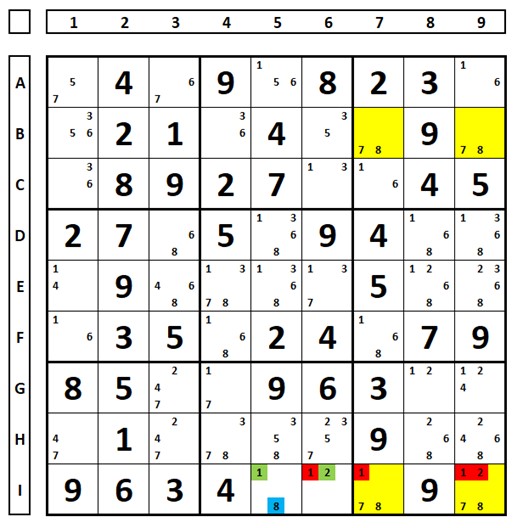
Retângulo Evitável com candidato ausente
No exemplo abaixo, não há o número “2”, na célula B8. Mas ao se escolher o número “2” na célula B7, cria-se o padrão mortal. Logo este número pode ser excluído na célula B7. O número “4” forma um X-Wing nas células amarelas.


Outro exemplo:
Na célula B7 não há o número “4” para formar o padrão mortal. Mas ao escolher-se o número “1” na célula B7, forma-se o padrão mortal, portanto este pode ser excluído.

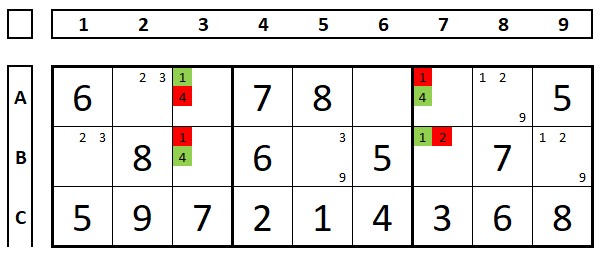
Observação:
Há outras situações em que se pode aproveitar esta técnica, os exemplos dados são suficientes para o leitor observar situações semelhantes. Mais um exemplo para encerrar esta técnica, no exemplo abaixo obrigatoriamente haverá em B1 ou C1 um número “3” ou um número “4”. Como há ambos os números em B2, nas demais células deste QM podem ser excluídos os números “3” e “4”.


