O XY-Wing funciona com um retângulo de 4 células com os pares trancados.

No Swordfish esta técnica é estendida para 9 células, alinhados em três linhas e três colunas. Não necessariamente é exigida a presença dos números nas nove células como será demonstrado adiante.
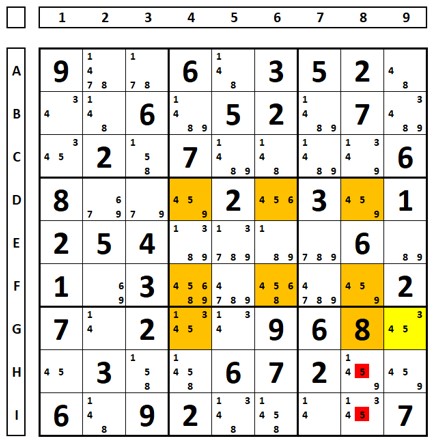
Abaixo um Swordfish clássico, onde as colunas 1, 4 e 7 possuem o número “7” fixados nas posições verdes. A escolha de um destes forcará a solução dos demais. Todos os números “7” em vermelho podem ser excluídos das demais células. Ou seja, todos os números entre duas células verdes ou que enxergue duas células verdes em uma linha ou coluna pode ser excluído. Deixando claro, o número “7” da célula B2 não pode ser excluído pois não está entre duas células verdes e nem enxerga duas células verdes na coluna 2 ou Linha B.
Como funciona? A escolha qualquer um dos números “7” como correto soluciona todas as demais células do Swordfish (células verdes).
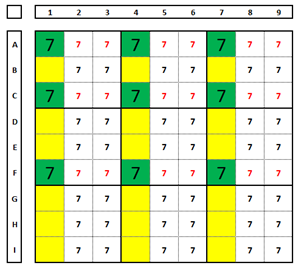
No Sudoku acima, se o número “7” for solução em A1, forma-se um X-Wing nas colunas 4 e 7. Teste para cada um dos números “7” e veja como a solução sempre estará entre eles.
Estes Sudoku clássicos são mais raros, os mais encontrados têm a formação 2x2x2, 3x3x2, 3x2x2, 2x3x2, 2x2x3. Exemplos:
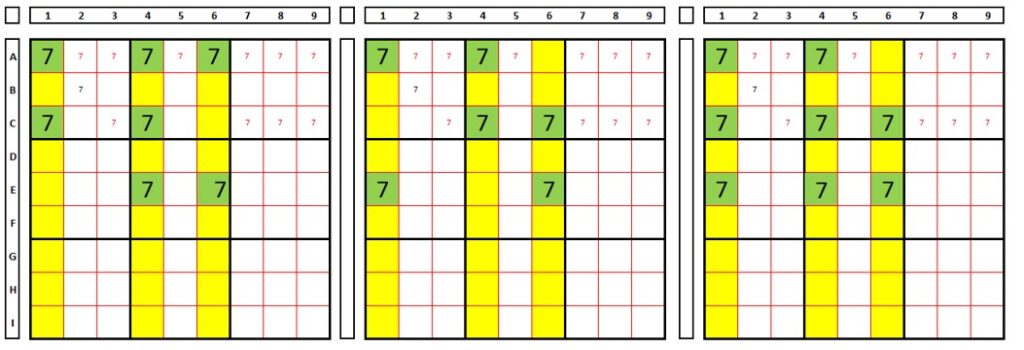
Assim como o XY-Wing necessita de uma cadeia fechada de 4 valores, um Swordfish necessita de uma cadeia fechada de 6.
No exemplo abaixo, em verde, 3x2x2, teste escolhendo I2 depois I5 como solução para o número “3”.

Exemplo 2 x 2 x2.

Exemplo 2 x 3 x 3.

Também chamada de "Finned Swordfish"
Chamadas de “finned”, esta extensão é uma variação das técnicas com nomes de peixes: Swordfish (peixe-espada) e Jellyfish (medusa) com um braço extra (chamado barbatana – ou “fin”).
Em outras palavras os Swordfish e jellyfish são peixes sem barbatanas(?). Porque têm estes nomes parece ser desconhecido.
Os “finned” Swordfish e Jellyfish pelo menos possuem uma barbatana (!). Será que nadam em círculos?
Indo ao Finned Swordfish.
Como funciona? Esta técnica é usada quando há uma célula “extra ” no swordfish. A célula extra deve estar na mesma linha (ou coluna) da formação swordfish. Se for escolhida a célula extra como verdadeira (solução do sudoku), quais células ela elimina? E se não for solução para o sudoku, quais são eliminadas? As células com a mesma resposta terão o candidato eliminado.
Conceitos (ver sudoku abaixo).
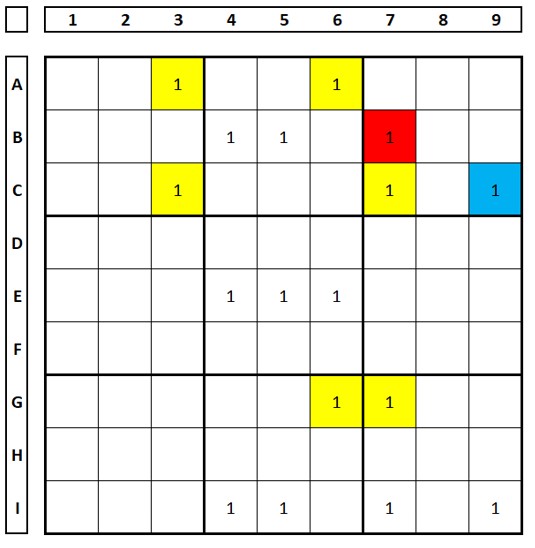
Como funciona? Esta técnica é usada quando há uma célula “extra ” (barbatana) no swordfish (pode haver duas, sempre no mesmo QM, será visto adiante). A célula extra deve estar na mesma linha (ou coluna) da formação swordfish. Se for escolhida a célula extra como verdadeira (solução do sudoku), quais células ela elimina? E se não for solução para o sudoku, quais são eliminadas? As células com a mesma resposta terão o candidato eliminado.
No Sudoku abaixo há o exemplo 2x3x2 (A3/A6, C3/C7+ C9, G6/G7). O número “1” na célula C9 não faria parte deste Swordfish. Conjunto base linhas A, C e G. Conjunto de cobertura colunas 3, 6 e 7. A eliminação ocorrerá na coluna 7, no QM3, onde está a célula extra. Usando a regra acima o número “1” da célula B7 é excluído. (Faça este teste: qualquer escolha do número “1” na linha G excluí este número na célula B7). Largue o lápis, só olhe.

Neste outro exemplo, pode-se formar o “peixe-espada” com o número “2” nas colunas 3, 5 e 8. No QM7, o número “2” da solução está contido no conjunto formado pelas células verdes ou estará na célula marrom. Com isto pode-se eliminar o número “2” da célula H2.
Conjunto base nas colunas 3, 5 e 8. Conjunto de cobertura nas linhas B, C e H. Logo a eliminação será na linha H do QM7 (onde está a célula extra).
Teste sua imaginação, considerando o número “2” como solução na célula H8 e depois B8 e veja o que acontece.

Outro exemplo, para o número “4”.

Um exemplo com dupla eliminação. No sudoku abaixo, olhando o número “9”, um Swordfish com conjunto de base nas colunas 1, 6 e 8 e conjunto de cobertura nas linhas A, B e H. A barbatana na célula G8 permite as duas eliminações nas linhas no conjunto de cobertura.
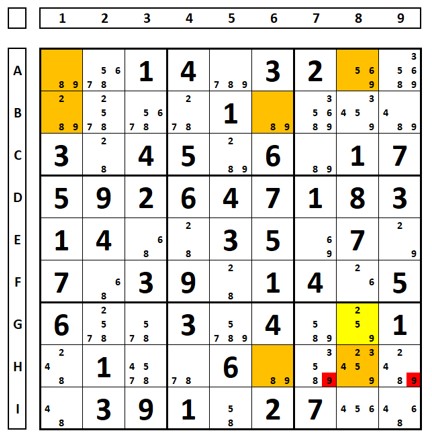
O mesmo acontece quando há duas células extras. Ou ambas são falsas ou uma é verdadeira (já que ambas não podem ser verdadeiras), permitindo as duas eliminações abaixo.
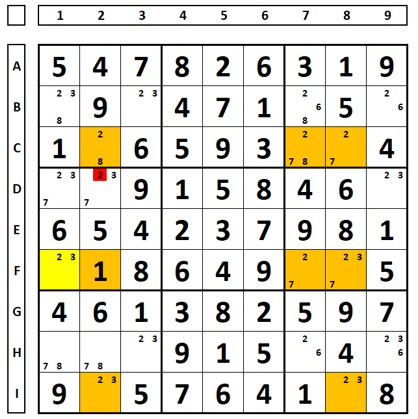
Para o número “3”. Conjunto base colunas 1, 3 e 6. Conjunto cobertura nas linhas B, F. G (onde haverá a eliminação no QM7, onde estão as duas células extras – barbatanas, no conjunto amarelo).
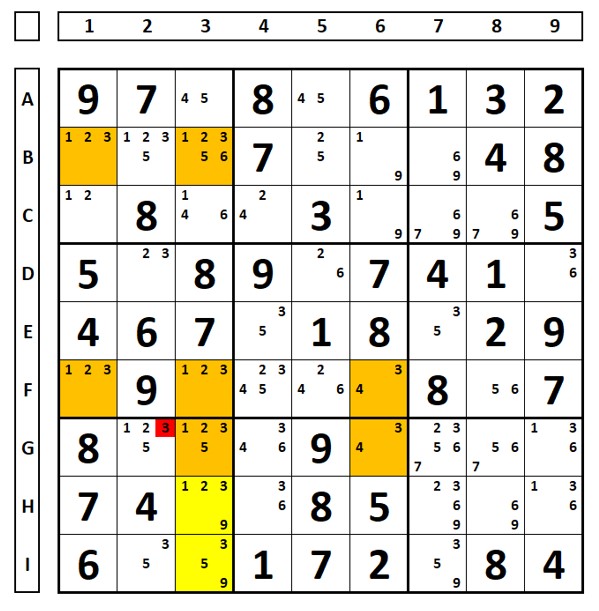
Para entender é necessário voltar aos X-Wing. No sudoku abaixo haveria um fillet X-Wing (conjunto base, linhas D e F, conjunto cobertura, colunas 3 e 9) se o número “2” estivesse na célula D3, o que excluiria o número “2” na célula F3. Mas não está. E se considerar a célula D1 como “barbatana” do “X-Wing” em rosa?
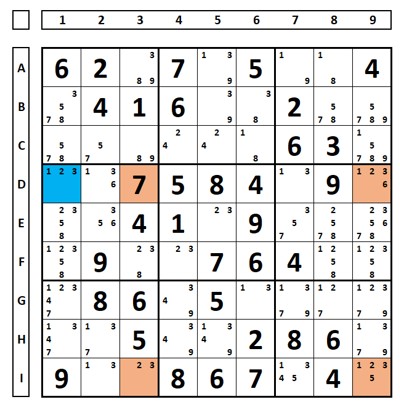
O que acontece se o número “2” for verdadeiro ou falso na barbatana (célula D1)? Em ambos os casos há exclusão deste número na célula F3.
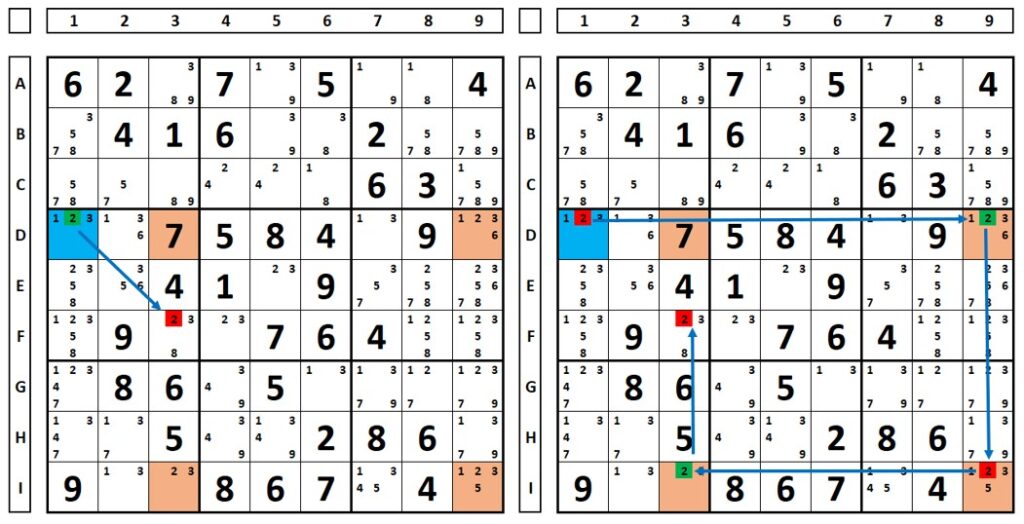
Neste outro exemplo ocorre o mesmo. Para o número “3”, X-Wing nas colunas 2 e 8. Este número ser verdadeiro ou falso na célula D3 elimina-o na célula F1.
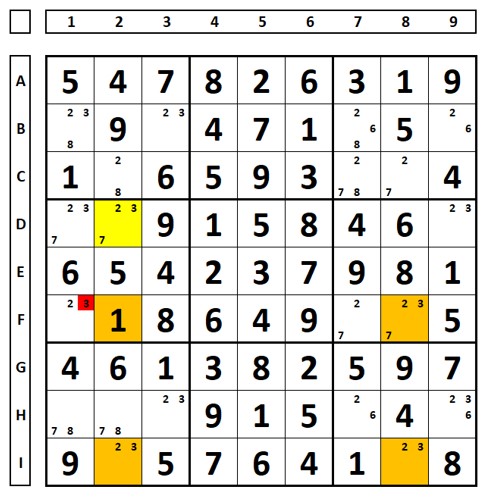
Examinando o número “2” no sudoku abaixo. Haveria um Swordfish nas células marrons (linhas C, F e I), caso não houvesse a pista “1” na célula F2. E há uma barbatana (“fin”, célula extra) na célula F1. Caso a célula F1 seja solução elimina o número “2” na célula D2. Caso não seja solução há a mesma eliminação pela formação de um Swordfish clássico (linhas C – C2, C7 e C8; F – F7 e F8; I – I2 e I8).
Outro exemplo. Conjunto base nas colunas 2, 6 e 8. Conjunto de cobertura nas linhas B, G e I. Permite duas exclusões.

Observe o sudoku abaixo, conjunto de base para o número “5” na linha e de cobertura nas coluna.