The XY-Wing works with a rectangle of 4 cells with locked pairs

In Swordfish, this technique is extended to 9 cells, aligned in three rows and three columns. The presence of numbers in all nine cells is not necessarily required, as will be demonstrated below.
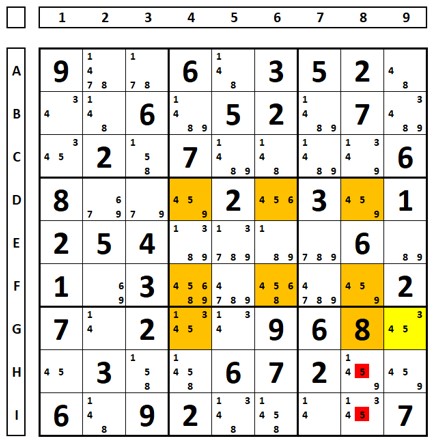
Below is a classic Swordfish, where columns 1, 4, and 7 have the number “7” fixed in the green positions. Choosing any of these numbers as the correct solution will force the solution of the others. All the “7” numbers in red can be excluded from the other cells. That is, all numbers between two green cells or that see two green cells in a row or column can be excluded. To be clear, the “7” in cell B2 cannot be excluded because it is not between two green cells and does not see two green cells in column 2 or row B.
How does it work? Choosing any of the “7” numbers as the correct solution solves all the other cells in the Swordfish (green cells).
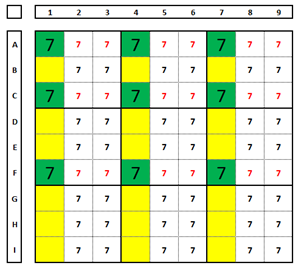
In the above Sudoku, if the number “7” is a solution in A1, an X-Wing is formed in columns 4 and 7. Test for each of the “7” numbers and see how the solution will always be between them.
These classic Sudoku puzzles are rarer, the most common formations are 2x2x2, 3x3x2, 3x2x2, 2x3x2, 2x2x3. Examples:
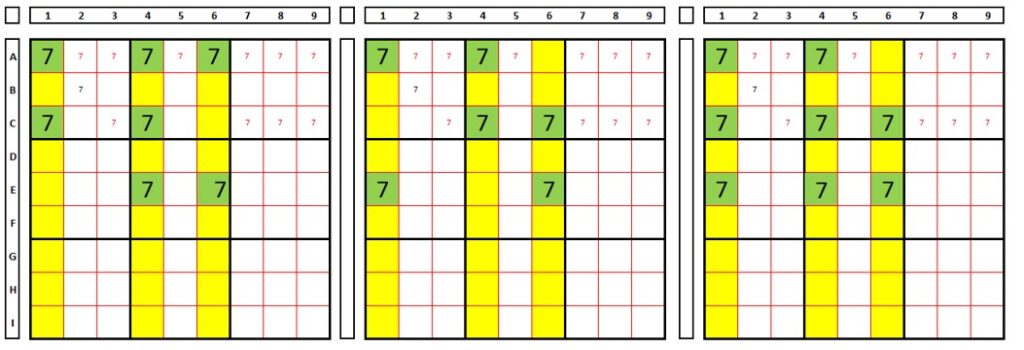
“Just like the XY-Wing needs a closed chain of 4 values, a Swordfish needs a closed chain of 6.
In the example below, in green, 3x2x2, test by choosing I2 then I5 as the solution for the number “3”:

Example 2 x 2 x2:

Example 2 x 3 x 3:

Also called "Finned Swordfish"
Called “finned”, this extension is a variation of the fish-named techniques: Swordfish and Jellyfish with an extra arm (called fin).
In other words, Swordfish and Jellyfish are fish without fins(?). Why they have these names seems to be unknown.
The “finned” Swordfish and Jellyfish at least have one fin (!). Do they swim in circles?
Let’s talk about the Finned Swordfish.
How does it work? This technique is used when there is an “extra” cell in the Swordfish formation. The extra cell must be in the same row (or column) as the Swordfish formation. If the extra cell is chosen as the true solution (for the Sudoku), which cells does it eliminate? And if it is not a solution for the Sudoku, which cells are eliminated? The cells with the same candidate will have that candidate eliminated.
Concepts (see sudoku below):
How does it work? This technique is used when there is an “extra” cell (fin) in the swordfish (there can be two, always in the same box, which will be seen later). The extra cell must be on the same row (or column) as the swordfish formation. If the extra cell is chosen as true (sudoku solution), which cells does it eliminate? And if it is not a solution for the sudoku, which ones are eliminated? The cells with the same answer will have their candidate eliminated..
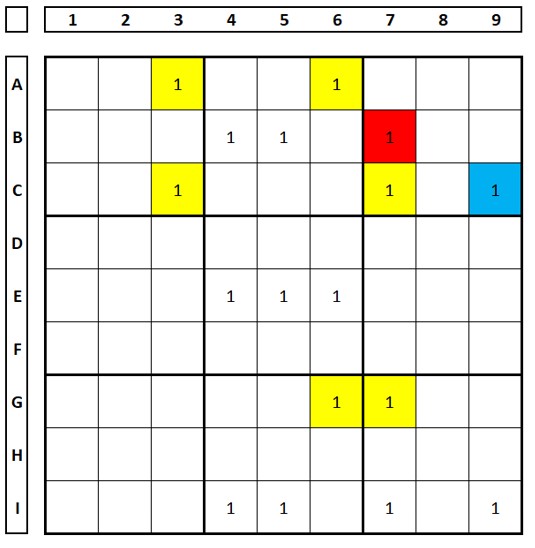
In the Sudoku below there is an example of a 2x3x2 formation (A3/A6, C3/C7+ C9, G6/G7). The number “1” in cell C9 would not be part of this Swordfish. The base set is rows A, C, and G. The covering set is columns 3, 6, and 7. The elimination will occur in column 7, in box 3, where the extra cell is located. Using the rule above, the number “1” in cell B7 is excluded. (Try this test: any choice of the number “1” in row G excludes this number in cell B7). Put down your pencil and just look at it.

In this other example, we can form the “swordfish” with the number “2” in columns 3, 5, and 8. In box 7, the number “2” of the solution is either in the set formed by the green cells or in the brown cell. This allows us to eliminate the number “2” from cell H2.
The base set is in columns 3, 5, and 8. The covering set is in rows B, C, and H. Therefore, the elimination will be in row H of box 7 (where the extra cell is located).
Test your imagination by considering the number “2” as a solution in cell H8 and then B8 and see what happens.

Another example, for the number “4”

Another example with double elimination. In the sudoku below, looking at the number ‘9’, a Swordfish with base set in columns 1, 6, and 8 and coverage set in rows A, B, and H. The fin in cell G8 allows for two eliminations in the rows of the coverage set:
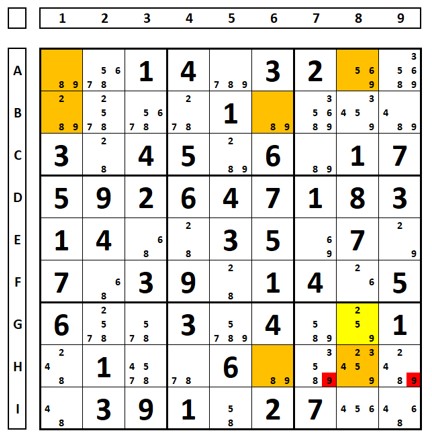
The same happens when there are two extra cells. Either both are false or one is true (since both cannot be true), allowing for the two eliminations below.
For the number “3”. Base set in columns 1, 3, and 6. Coverage set in rows B, F, G (where there will be elimination in box 7, where the two extra cells – fins, in the yellow set – are located).
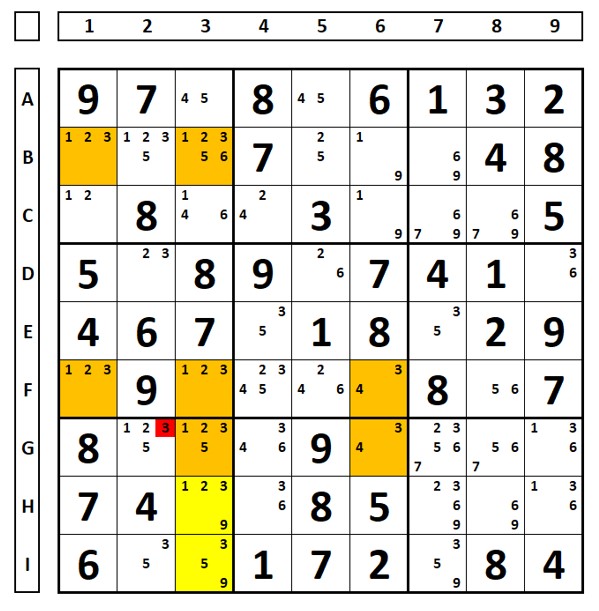
To understand, it is necessary to go back to X-Wings. In the Sudoku below, there would be an X-Wing fillet (base set, rows D and F, covering set, columns 3 and 9) if the number “2” was in cell D3, which would exclude the number “2” in cell F3. But it is not. And if we consider cell D1 as the “fin” of the pink “X-Wing”?
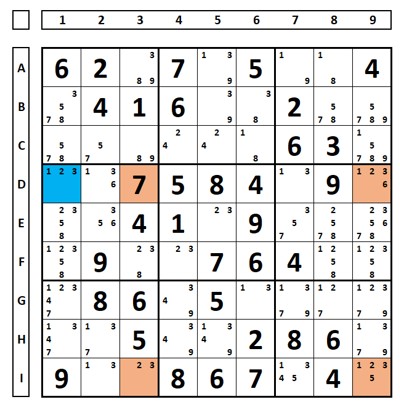
What happens if the number “2” is true or false in the “fin” (cell D1)? In both cases, this number is excluded from cell F3:
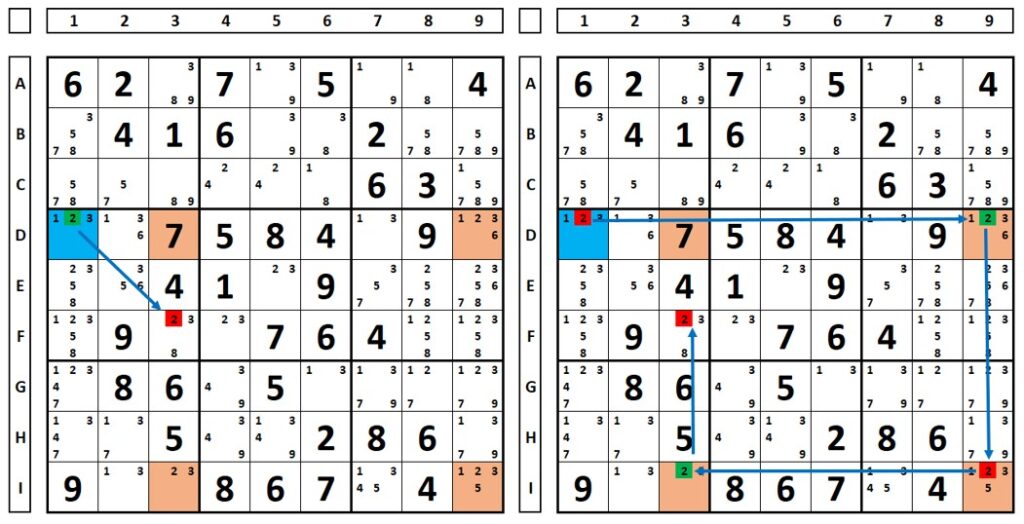
In this other example, the same thing happens. For the number “3”, there is an X-Wing in columns 2 and 8. Whether this number is true or false in cell D3 eliminates it in cell F1:
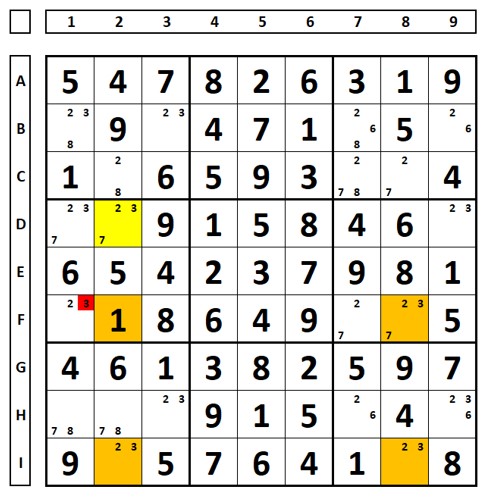
Examining the number “2” in the Sudoku below. There would be a Swordfish in the brown cells (rows C, F, and I), if there were no clue “1” in cell F2. And there is a “fin” (extra cell) in cell F1. If cell F1 is a solution, it eliminates the number “2” in cell D2. If it is not a solution, there is the same elimination by forming a classic Swordfish (rows C – C2, C7, and C8; F – F7 and F8; I – I2 and I8):
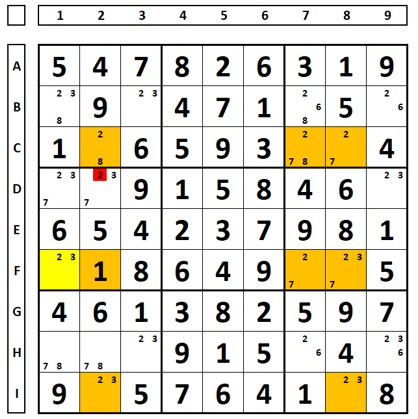
Another example. Base set in columns 2, 6, and 8. Covering set in rows B, G, and I. Allows for two eliminations:

Observe the Sudoku below, base set for the number “5” in the row and covering set in the column: